تحلیل داده پانلی در SPSS چگونه است؟

تحلیل داده پانلی در SPSS چگونه است؟

«داده‌های پانلی» (Panel Data) یا «سری زمانی مقطعی» (Cross-Sectional Time series) در حوزه‌های مرتبط با مسائل «اقتصاد سنجی» (Econometric) ریشه داشته و به سری‌های زمانی چند بُعدی اختصاص یافته‌اند. تحلیل داده پانلی پیچیده بوده و بار محاسباتی زیادی دارند. بنابراین اغلب از نرم‌افزارهای محاسبات آماری مانند SPSS برای تحلیل آن‌ها استفاده می‌شود. به همین علت در این نوشتار نیز به داده پانلی و تحلیل آن در SPSS می‌پردازیم و با ذکر مثالی در این حوزه، موضوع را روشن‌تر می‌کنیم.

تحلیل داده پانلی در SPSS

تجزیه و تحلیل «داده‌های پانلی» (Panel Data)، که به عنوان «تجزیه و تحلیل سری زمانی مقطعی» (cross-sectional time-series analysis) نیز شناخته می‌شود، تکنیکی است که در آن برای مثال، گروهی از افراد، در بیش از یک موقعیت مورد بررسی و تحلیل قرار می‌گیرند. تحقیق روی داده پانلی اساساً معادل «مطالعات طولی» (longitudinal studies) هستند، هر چند ممکن است متغیرهای پاسخ بسیاری در هر زمان مشاهده شوند.

اولین بار بررسی چنین داده‌هایی براساس مطالعه‌ای در سال ۱۹۹۶ در مورد اثر بخشی بسته‌های استروژن در درمان افسردگی پس از تولد، صورت گرفت. نتایج این تحقیق توسط گروهی از آمارشناسان و محققین (Gregoire، Kumar Everitt، Henderson and Studd) منتشر شد.

نمونه‌ای از زنان که به تازگی زایمان انجام داده‌اند انتخاب شده و به طور تصادفی در یک گروه کنترل یا دارونما (group = 0 ،n = 27) و گروه بسته استروژن (group= 1 ،n = 34) قرار گرفتند. قبل از اولین درمان، میزان افسردگی همه بیماران با استفاده از «مقیاس افسردگی پس از زایمان ادینبورگ» (EPDS یا Edinburgh Postnatal Depression Scale) اندازه‌گیری شد. با شروع درمان، داده‌های EPDS به مدت شش ماه و بطور ماهانه جمع آوری شد. توجه داشته باشید که نمرات بالاتر در EDPS نشان دهنده سطح بالاتر افسردگی است.

برای دریافت فایل اطلاعاتی این مجموعه داده،‌ به نام depress-3.sav، با قالب فشرده می‌توانید اینجا کلیک کنید. واضح است که پس از خارج کردن فایل از حالت فشرده، قادر به بارگذاری آن در نرم‌افزار SPSS خواهید بود. کد زیر در محیط Syntax در نرم‌افزار SPSS برای بارگذاری آن از طریق اینترنت پیشنهاد شده است.

get file = 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/depress-3.sav'.

البته می‌توانید با فرض قرارگیری فایل در درایو :D، از کد زیر برای فراخوانی استفاده کنید.

get file = 'D:\depress-3.sav'.

ابتدا بهتر است به این مجموعه داده نگاهی بیاندازیم.

بررسی داده‌های پانلی در SPSS

پس از بارگذاری فایل depress-3 در SPSS، در «پنجره ویرایشگر داده» (Data Editor)، اطلاعات مربوط به ۶۱ = ۳۴+۲۷ بیمار مشخص می‌شود. به تصویر ۱ توجه کنید.

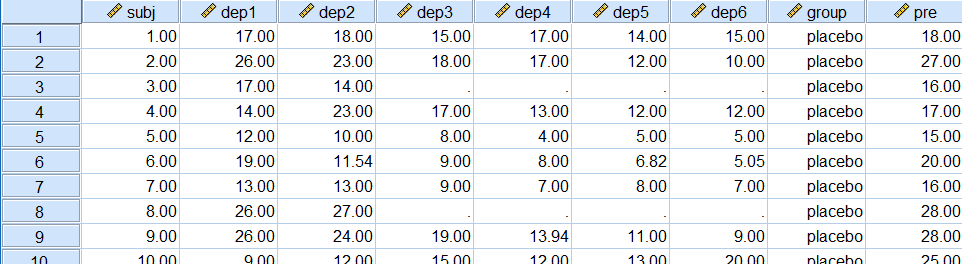
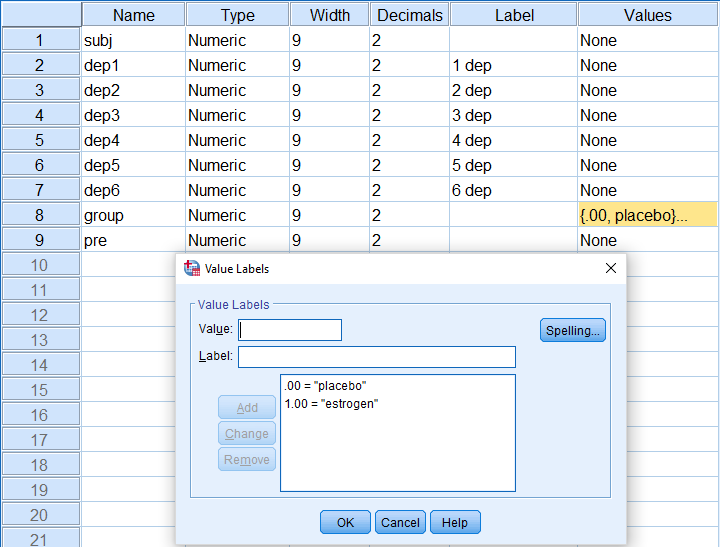
همچنین متغیرهای به کار رفته در این مجموعه داده در تصویر ۲ نمایش داده شده است. متغیر subj، شماره یا کد هر بیمار است. dep1 تا dep6 مقدار افسردگی در هر یک از ماه‌ها ( ۱ تا ۶) را نشان می‌دهد. group‌ برای مشخص کردن گروه بیمار، یعنی گروه کنترل دارونما (با کد placebo) و گروه استروژن (با کد estrogen) با مقادیر ۰ و ۱ به کار رفته است. در ستون آخر یعنی pre نیز مقدار شاخص EDPS را  قبل از شروع دوره درمان، مشاهده می‌کنید.

البته واضح است که با گذر زمان، میزان افسردگی بعد از زایمان کاهش خواهد یافت. ولی می‌خواهیم در این مسئله، به اثر دارو استروژن بپردازیم و سرعت یا اثربخشی این دارو را در کاهش میزان افسردگی مشخص کنیم. به منظور جداسازی هر یک از گروه‌ها و محاسبه شاخص‌های آمار توصیفی، از دستورات زیر استفاده کرده‌ایم.

sort cases by group.
split file by group.
descriptives var = pre dep1 dep2 dep3 dep4 dep5 dep6.
split file off.

نتیجه به صورت یک جدول به مانند تصویر ۳ خواهد بود.

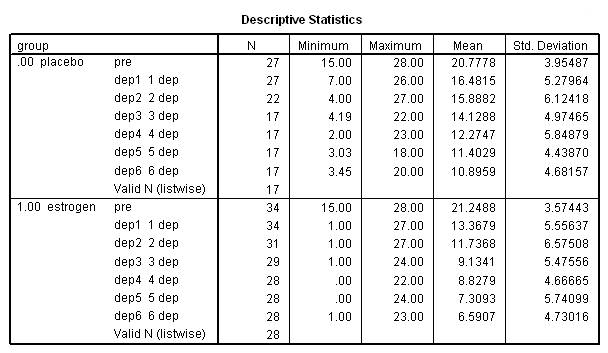
همانطور که می‌بینید، در گروه کنترل فقط ۱۷ بیمار تا آخر آزمایش مورد بررسی قرار گفته‌اند. همچنین در گروه estrogen نیز تعداد بیماران که طرح تحقیق را تا انتها همراهی کرده‌اند، فقط ۲۸ نفر هستند. در نتیجه در اینجا فقط ۴۵ = ۱۷+۲۸ نفر در کل، تا پایان تحقیق مورد بررسی قرار گرفته‌اند در حالیکه نمونه اصلی شامل ۶۱ نفر بوده است.

توجه داشته باشید که در انتهای کد، مجموعه داده را از حالت تفکیک (split) خارج کرده‌ایم تا برای مراحل بعدی مشکلی پیش نیاید.

همچنین با اندازه‌گیری همبستگی بین مقدار شاخص افسردگی در بین دوره‌های مختلف برای بیماران، به درک مناسبی در مورد میزان ارتباط زمانی بین آن‌ها خواهیم رسید. شاخص «همبستگی پیرسون» (Pearson Correlation) را به کمک کد زیر محاسبه خواهیم کرد.

correlations var = pre dep1 dep2 dep3 dep4 dep5 dep6.

جدول ضرایب همبستگی دو به دو متغیرهای مربوط به میزان افسردگی، محاسبه شده و در تصویر ۴، قابل مشاهده است.

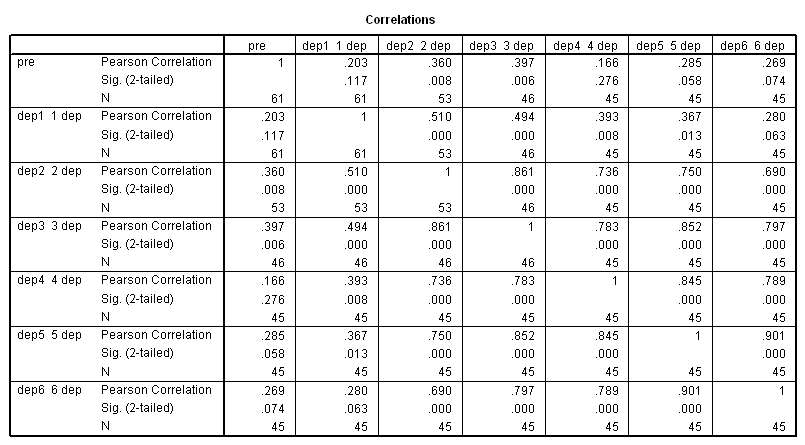
همین جدول را به صورت گرافیکی نیز نشان خواهیم داد. به این ترتیب رابطه خطی بین متغیرها بهتر دیده خواهد شد. به این منظور از کد زیر و رسم نمودار با دستور graph در SPSS استفاده خواهیم کرد.

graph
 /scatterplot(matrix) = pre dep1 dep2 dep3 dep4 dep5 dep6.

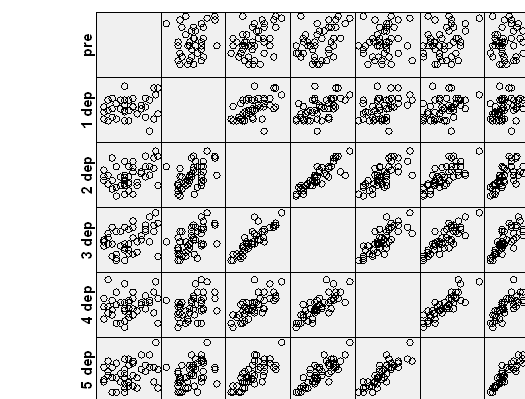
نموداری مطابق با تصویر ۵، ظاهر خواهد شد. در اکثر موارد بین متغیرها یک رابطه خطی دیده می‌شود. البته میزان افسردگی در اول دوره (قبل از اجرای درمان) با هیچ یک از متغیرهای دیگر، رابطه خطی ندارد. این موضوع را جدول ضرایب همبستگی نیز مورد آزمون قرار داده و برای بیشتر حالت‌ها، مقدار sig بزرگتر از ۰٫۰۵ شده است. ولی در عوض بین متغیرهای مربوط به درمان در اکثر مواقع، مقدار Sig کمتر از ۰٫۰۵ بوده که نشانگر معنی‌دار بودن ضریب همبستگی خطی پیرسون دارد. این نمودارها نشان می‌دهند که بین دوره‌های اندازه‌گیری افسردگی بعد از زایمان، همبستگی خطی و مثبتی وجود دارد. هر چه دوره‌ها به یکدیگر نزدیکتر باشند، این وابستگی نیز بیشتر است. بنابراین همبستگی با یک وقفه (lag) زمانی برابر با ۱، اتفاق می‌افتد.

در انتهای این بخش نیز با استفاده از آزمون تی دو نمونه مستقل، بین دو گروه کنترل و استروژن، برابری میانگین‌های میزان افسردگی با شاخص EPDS برای دوره قبل از درمان را مورد بررسی قرار می‌دهیم. به این منظور از کد زیر در Syntax استفاده کرده‌ایم.

t-test groups = group(۰ ۱)
 /var = pre.

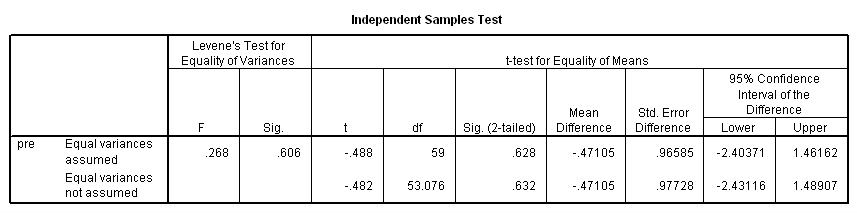
نتیجه اجرای این قطعه کد در تصویر ۶ دیده می‌شود. مشخص است که چه در حالت «برابری واریانس» (Equal variances assumed) یا «نابرابری آن‌ها» (Equal variance not assumed)، فرض صفر رد می‌شود. در هر دو حالت (سطر اول و دوم) مقدار Sig بزرگتر از ۰٫۰۵ است.

پس اختلاف معنی‌داری بین دو گروه (دارو نما و داروی استروژن) قبل از تیمار یا درمان افسردگی وجود ندارد. پس به نظر می‌رسد که هر دو گروه از نظر میزان افسردگی، دارای مقداری یکسان هستند و می‌توان بیماران را یکسان در نظر گرفت. این موضوع نشان می‌دهد که در انتخاب نمونه‌ها، هیچ اریبی یا بایاس (Bias) وجود ندارد.

تحلیل داده پانلی در SPSS با روش GEE

برای استفاده از داده پانلی در SPSS‌ با تکنیک GEE، باید آن‌ها را تغییر وضعیت داده و ساختار آن‌ها را عوض کنیم. به این ترتیب با استفاده از دستور vartocases که در ادامه مشاهده می‌کنیم، تغییری در شیوه قرارگیری داده‌ها در جدول اطلاعاتی ایجاد می‌کنیم. به این ترتیب جای متغیرها و مشاهدات در جدول اطلاعاتی تغییر خواهد کرد.

varstocases
 /make dep from dep1 dep2 dep3 dep4 dep5 dep6
 /index = visit.

با اجرای این کد، متغیرهای جدیدی به نام visit و dep ساخته می‌شوند که به ترتیب، ماه مربوط به اندازه‌گیری افسردگی و اندازه افسردگی را برای هر بیمار (بسته به گروه کنترل یا استروژن) نمایش می‌دهند. در تصویر ۷، نمایی از مقادیر با تغییر ساختار را مشاهده می‌کنید.

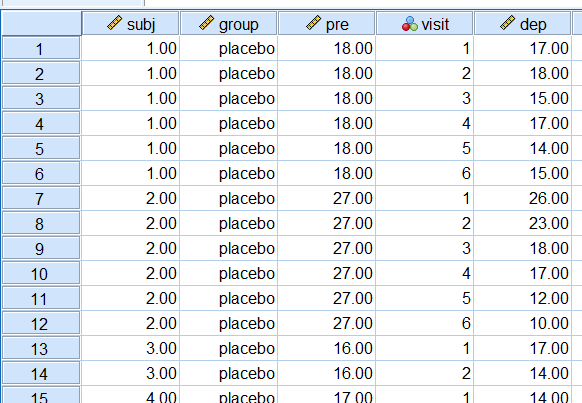
البته نتایج مربوط به اجرای کد به مطابق با تصویر ۸ در پنجره خروجی SPSS ظاهر خواهد شد. همچنین متغیرهای به کار رفته در ساختار اولیه و همچنین متغیرهای تولید شده در حالت تغییر ساختار، در جدولی با نام Processing Statistics، دیده می‌شود.

تحلیل داده پانلی براساس آنالیز واریانس با مقادیر تکراری

به یاد دارید که هدف از اجرای تحلیل داده پانلی در SPSS، نمایش اثر بخشی دارو در درمان افسردگی پس از زایمان بود. از آنجایی که هر آزمودنی در بیش از یک مرحله اندازه‌گیری شده بود، می‌توان چنین کاری را با استفاده از «تحلیل واریانس با مقادیر تکراری» (Repeated Measures Analysis of Variance) نیز انجام داد. کد زیر به این منظور نوشته شده است.

unianova dep by visit group subj
 /test =group vs subj(group)
 /design = group visit group*visit subj(group).

نتیجه اجرا و خروجی این دستورات در تصویر ۹ دیده می‌شود.

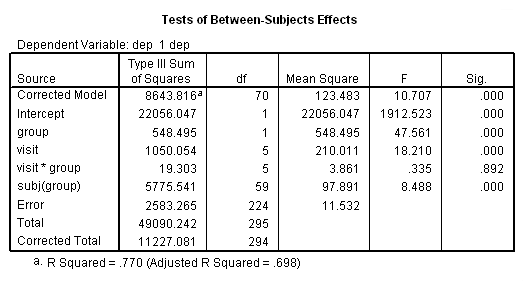
بر طبق تصویر ۹، به جر اثرات متقابل، همه اثرات اصلی، معنی‌دار محسوب می‌شوند. در تصویر ۱۰، با توجه به مقدار Sig.= 0.۰۲۱ مشخص است که بین دو گروه، از لحاظ میانگین شاخص افسردگی، تفاوت معنی‌داری وجود دارد.

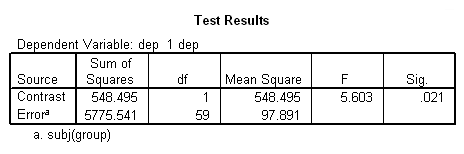
تحلیل داده پانلی براساس مدل رگرسیونی

با توجه به شیوه جدید نمایش داده‌ها، مشخص است که سطرهای جدول اطلاعاتی، نسبت به یکدیگر مستقل هستند. به این ترتیب با استفاده از مدل رگرسیونی نیز داده‌های پانلی را می‌توان تحلیل نمود. البته به یاد داشته باشید که نرمال بودن متغیر پاسخ (یا جمله خطا) از شرط‌های اصلی در مدل رگرسیونی OLS است.

کدهای لازم برای اجرای مدل رگرسیونی در ادامه دیده می‌شوند. مشخص است که متغیر وابسته dep‌ و متغیرهای مستقل نیز pre ،group و visit هستند.

regression
 /dependent = dep
 /method = enter pre group visit.

نتیجه اجرای کد با نمایش جدولی به نام Model Summary آغاز می‌شود. مقادیر این جدول هر چه بزرگتر و نزدیک به ۱ باشند، نشانگر مناسب بودن مدل خواهند بود. با توجه به کوچک بودن ضریب همبستگی (R=.۵۷۶) و ضریب تعیین (R Square=.۳۳۱)، مدل حاصل مناسب به نظر نمی‌رسد.

در جدول بعدی که در تصویر ۱۲ دیده می‌شود، «جدول آنالیز واریانس» (ANOVA) برای مدل رگرسیونی ظاهر شده است. البته در اینجا مقدار Sig=.۰۰۰‌ نشانگر معنی‌دار بودن مدل تحلیل واریانس است.

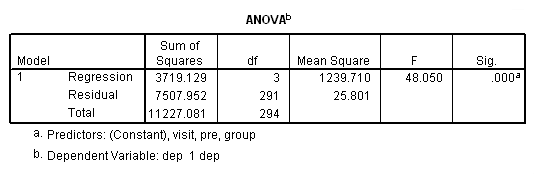
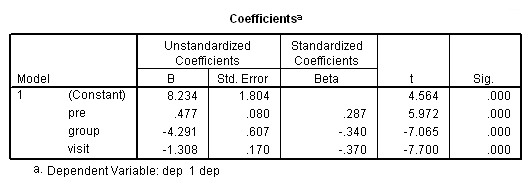
در انتها نیز جدول Coefficients، یا برآورد ضریب‌های مدل رگرسیونی را مطابق با تصویر ۱۳ می‌بینید. واضح است که همه مقادیر یعنی عرض از مبدا (Constant) و ضریب متغیر pre ،group و visit از لحاظ آماری و در سطح خطای ۰٫۰۵، معنی‌دار هستند.

نکته: از آنجایی که آزمون‌های مربوط صحت مدل رگرسیون مانند «نرمال‌بودن باقی‌مانده‌ها» (Normality of Residuals)، «ثابت بودن واریانس» (Constant Variance) و «همخطی» (Colinearity) صورت نگرفته، ممکن است این نتایج گمراه کننده باشند.

تحلیل داده پانلی با تکنیک GEE

در این مرحله، آماده هستیم که از تکنیک ناپارامتری GEE برای تحلیل داده پانلی استفاده کنیم. در محیط SPSS برای کار روی داده پانلی نمی‌توان از منوها استفاده کرد ولی کدنویسی در پنجره Syntax برای اجرای چنین تحلیلی مناسب است.

تابع genlin در SPSS برای استفاده از تکنیک GEE در نظر گرفته شده که در ادامه متن به بررسی آن و شناسایی پارامترهایش خواهیم پرداخت. این دستور به ما اجازه می‌دهد تا ساختارهای مختلف برای ماتریس کوواریانس یا ماتریس «همبستگی» (Correlation) را با استفاده از گزینه corrtype در زیرفرمان repeated مشخص کنیم.

ابتدا با یک ساختار کوواریانس بدون همبستگی یا همان استقلال شروع خواهیم کرد. البته لزومی ندارد که حتما این ساختار مناسب باشد ولی برای شروع کار بد نیست که با آن محاسبات را آغاز کنیم زیرا به ما امکان مقایسه نتایج با نتایج رگرسیون OLS (که در قسمت قبل اجرا شد) را می‌دهد. گزینه workingcorr در زیرفرمان print نیز به منظور «نمایش ماتریس همبستگی کاری» (working correlation matrix) در نظر گرفته شده است. توجه داشته باشید که این گزینه فقط در صورت استفاده از زیرفرمان repeated در دسترس خواهد بود.

نکته: دستور genlin در SPSS برای نسخه ۱۵ به بعد قابل اجرا است. همچنین به روزرسانی و رفع اشکال نیز در نسخه ۱۶ صورت گرفته است. اگر از نسخه‌های قدیمی‌تر این نرم افزار استفاده می‌کنید، امکان به کارگیری فرمان genlin را ندارید.

تحلیل داده پانلی با ساختار استقلال برای ماتریس همبستگی

دستورات و کد زیر در محیط Syntax به منظور اجرای مدل GEE روی داده‌های مربوط به درمان افسردگی زایمان به کار گرفته شده. «تابع پیوند» (link function)، «تابع همانی» (identity) و توزیع نیز «نرمال» (Normal Distribution) فرض شده است.

genlin dep with pre visit group
 /model pre group visit distribution = normal link = identity
 /repeated subject = subj
 /print modelinfo cps solution workingcorr.

همانطور که می‌بینید، متغیرهای به کار رفته در مدل GEE، ستون pre ،group و visit هستند. در انتها نیز برای چاپ، جدول خلاصه مشاهدات (cps) یا همان case process summary و پاسخ (solution) و ماتریس همبستگی (workingcorr) درخواست شده است. نتایج را در تصویرهای ۱۴ تا ۱۷ مشاهده می‌کنید.

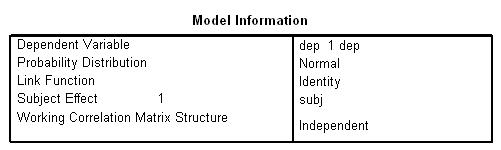
در تصویر ۱۴ در هر بخش، اطلاعاتی در مورد پارامتر یا پارامترهای به کار رفته در GEE دیده می‌شود. برای مثال «متغیر وابسته» (Dependent Variable) همان متغیر dep (با برچسب ۱dep) مشخص شده است. همچنین توزیع و «تابع پیوند» (link function) و اثرات اصلی (Subject Effect) مورد بررسی قرار گرفته است. در انتها نیز در بخش Working Correlation Matrix Structure ساختار ماتریس همبستگی، مستقل بودن (Independent) را تعیین کرده است.

در تصویر ۱۵ و در ستون N، تعداد مشاهدات معتبر (include) و همچنین مشاهدات با مقدار گمشده (exclude) که از تحلیل کنار گذاشته می‌شوند، نمایش داده شده و در سطر Total نیز کل بیماران دیده می‌شود. از آنجایی که ساختار داده‌ها را تغییر داده‌ایم، مقادیر گمشده در این جا دیده نمی‌شوند و همه مشاهدات دارای متغیرهایی با مقدار مشخص هستند.

در ستون Percent، درصد هر یک از گزینه‌ها نسبت به کل مشاهدات، محاسبه شده است. واضح است که هیچ مقدار گمشده‌ای وجود نداشته و گرنه آن مشاهده در تحلیل، کنار گذاشته می‌شود.

در تصویر ۱۶ نیز مشخصات ماتریس کوواریانس یا همبستگی ظاهر شده است. همانطور که می‌بینید، ۶۱ بیمار مورد بررسی قرار گرفته‌اند. ولی توجه داشته باشید که تعداد مشاهدات ۲۹۵ مورد است، زیرا هر نفر در دوره‌های ماهانه به طول شش ماه مورد بررسی و اندازه‌گیری قرار گرفته است. البته بعضی از آن‌ها، در بعضی از دوره‌ها، مورد اندازه‌گیری قرار نگرفته‌اند در نتیجه از طرفی تعداد سطوح (Number of Levels) نیز برابر با ۶۱ است. تعداد سطوح اندازه برای متغیر اثر نیز از ۱ تا ۶ است. بنابراین ابعاد ماتریس همبستگی ۶ در ۶ خواهد بود. به یاد دارید که ماتریس همبستگی برای عامل‌ها، یک ماتریس مربعی است.

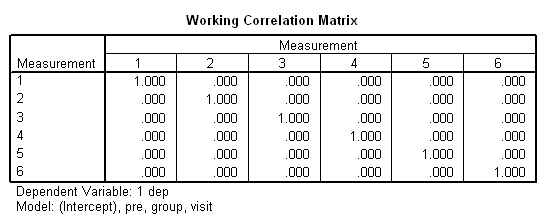
در تصویر ۱۷ نیز ساختار ماتریس همبستگی با توجه به شرط استقلال، آورده شده است. از آنجایی که فرض بر استقلال در بین سطوح عامل برقرار است، عناصر قطر اصلی برابر با ۱ و عناصر خارج از قطر، همگی صفر هستند تا نشانگر مستقل بودن آن‌ها باشد.

توجه داشته باشید که جدول پاسخ برای پارامترهای مدل نیز درست به مانند مدل رگرسیونی خواهد بود. بنابراین در اینجا از نمایش خروجی آن اجتناب می‌کنیم.

نکته: تجزیه و تحلیل و مدل ارائه شده با مدل‌های قسمت قبل، نتایج یکسان اما احتمالاً نادرست به همراه داشت. موضوع مشترک در بین آنها این است که همه آنها تصور می‌کنند مشاهدات درون موضوعات، مستقل هستند. به نظر می‌رسد این امر از نظر ظاهری بسیار بعید باشد. زیرا مقادیر مقیاس افسردگی به احتمال زیاد از یک اندازه در یک ماه نسبت به ماه قبل باید کاهش داشته باشند. پس شرط استقلال نمی‌تواند صحت داشته باشد.

تحلیل داده پانلی با ساختار تعویض‌پذیری برای ماتریس همبستگی

این بار با استفاده از «تقارن مرکب» یا «شرط تعویض‌پذیری» (Exchangeable) برای ساختار همبستگی کمک گرفته و این داده‌ها را تجزیه و تحلیل می‌کنیم. تعویض‌پذیری با استفاده از گزینه exchangeable در پارامتر corrtype حاصل و محاسبات براساس آن صورت می‌گیرد.

genlin dep with pre visit group
 /model pre visit group distribution = normal link = identity
 /repeated subject = subj corrtype = exchangeable
 /print modelinfo cps solution workingcorr.

نتیجه اجرای کد بالا، در SPSS، جدول‌هایی درست به مانند حالت قبل ایجاد می‌کند که به علت یکسان بودن بعضی از مقادیر آن‌ها، فقط در ادامه، فقط خروجی‌هایی را معرفی خواهیم کرد که شامل مقادیر متفاوت باشند. واضح است ابعاد ماتریس هبمستگی در حالت تعویض‌پذیر با حالت استقلال تفاوتی ندارد و فقط مقادیر درون ماتریس تغییر خواهند داشت.

از آنجایی که پاسخ‌ها (solution) نیز در دستور print به عنوان پارامتر، ذکر شده، برآورد ضرایب مدل مطابق با تصویر ۱۸، بدست آمده و در خروجی ظاهر خواهد شد.

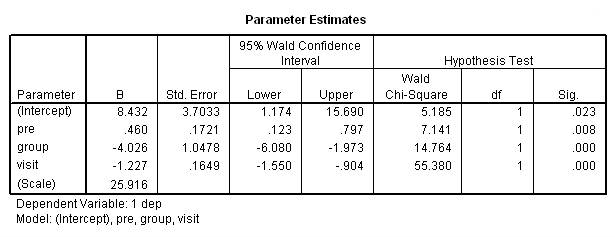
در ستون Sig مشخص است که همگی این ضرایب از لحاظ آماری، معنی‌دار بوده و صفر بودن آن‌ها در سطح خطای ۰٫۰۵، رد می‌شود. اثر متغیر group منفی است. به این معنی که برای گروه ۱ (کسانی که داروی استروژن مصرف کرده‌اند) میزان افسردگی کاهش خواهد داشت. از طرفی visit نیز با ضریب منفی تعیین شده که آن هم نشانگر کاهش شاخص افسردگی با گذشت زمان است. تنهای متغیری که ضریب مثبت دارد، pre است که همان میزان افسردگی در دوره قبل از درمان است. این ویژگی‌ها، به نظر عاقلانه می‌رسند، هر چند که در مدل رگرسیونی نیز چنین وضعیتی حاصل شده بود.

در تصویر ۱۹ نیز ساختار ماتریس همبستگی را مشاهده می‌کنید. از آنجایی که شرط تعویض‌پذیری یا تقارن وجود دارد، همه ضرایب همبستگی بین متغیر سطوح برابر هستند و فقط قطر اصلی که نشانگر همبستگی یک متغیر با خودش است، مقدار یک خواهد داشت.

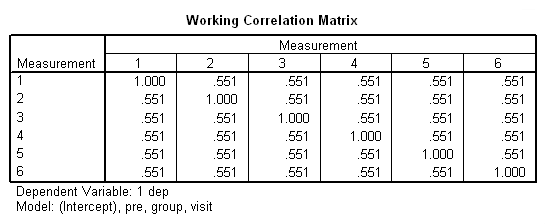
هر چند این ساختار بهتر از قبل عمل کرده است ولی هنوز به نقطه بهینه نرسیده‌ایم. پس کار را با استفاده از یک ساختار دیگر برای ماتریس همیستگی ادامه خواهیم داد.

تحلیل داده پانلی با ساختار اتورگرسیو مرتبه اول برای ماتریس همبستگی

بهتر است با توجه به وقفه یا lag یک مرحله‌ای، از یک مدل اتورگرسیو مرتبه ۱ برای ماتریس همبستگی در تحلیل داده پانلی استفاده کنیم. کدهای مربوط به این محاسبه در ادامه دیده می‌شود.

genlin dep with pre visit group
 /model pre group visit distribution = normal link = identity
 /repeated subject = subj corrtype = ar(۱)
 /print modelinfo cps solution workingcorr.

مشخص است که گزینه (corrtype = ar(۱ این عمل را انجام داده است. خروجی‌های جدید در تصویرهای ۲۰ و ۲۱ دیده می‌شوند. ابتدا نگاهی به برآورد پارامترهای می‌اندازیم. هر چند مقدار پارامتر در ستون B از جدول Parameter Estimates تغییر زیادی نداشته ولی انحراف استاندارد (std. Error) برای هر یک از پارامترها، کاهش یافته است. البته باز مشخص است که مقدار Sig نشانگر معنی‌داری همه پارامترها است.

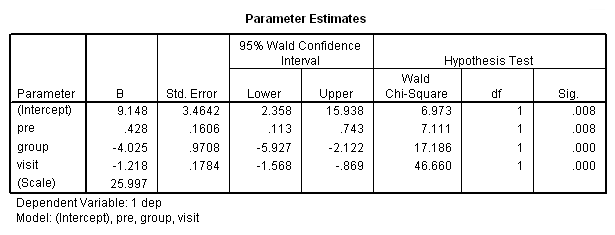
در تصویر ۲۱ نیز ساختار ماتریس همبستگی را براساس برآورد ضرایب همبستگی بین متغیرها، محاسبه و نمایش داده شده. همانطور که می‌بینید، هر چه وقفه زمانی بین اندازه‌گیری‌ها بیشتر شود، همبستگی بین آن‌ها کاهش می‌یابد. همین امر برای استفاده از مدل اتورگرسیو، دلیل مناسبی خواهد بود.

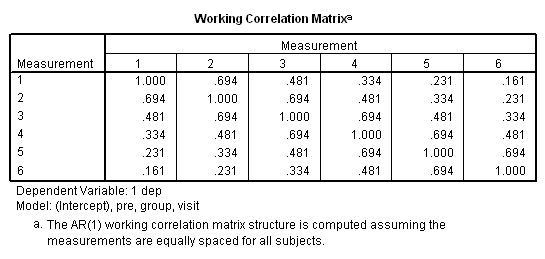
نکته: در خروجی تصویر ۲۱، نکته‌ای را باید در نظر گرفت که SPSS با فرض یکسان بوده فاصله زمانی بین سطوح متغیرهای عامل، مدل اتورگرسیو را در نظر گرفته و ضرایب همبستگی را محاسب کرده است. البته این امر در مسئله ما نیز لحاظ شده بود.

تحلیل داده پانلی با ساختار اتورگرسیو و اثرات متقابل

این بار با استفاده از اثرات متقابل گروه و زمان یا دوره اندازه‌گیری شاخص افسردگی بعد از زایمان EDPS، عمل کرده و ترکیب این دو متغیر را نیز در مدل به کار خواهیم گرفت. البته همچنان مدل اتورگرسیو مرتبه اول را برای ساختار ماتریس همبستگی به کار خواهیم بست.

کد زیر به منظور محاسبه متغیر جدید gxv و به کارگیری آن به عنوان متغیر عامل اثرات متقابل نوشته شده و پس از آن مدل GEE و برآورد پارامترها صورت گرفته است.

compute gxv = group*visit.
exe.
genlin dep with pre visit group gxv
 /model pre group visit gxv distribution = normal link = identity
 /repeated subject = subj corrtype = ar(۱).

در تصویر ۲۲، خروجی حاصل از محاسبه پارامترها را مشاهده می‌کنید. واضح است که با توجه به مقدار Sig، اثر متقابل گروه و متغیر دوره اندازه گیری، در مدل، معنی‌دار نیست.

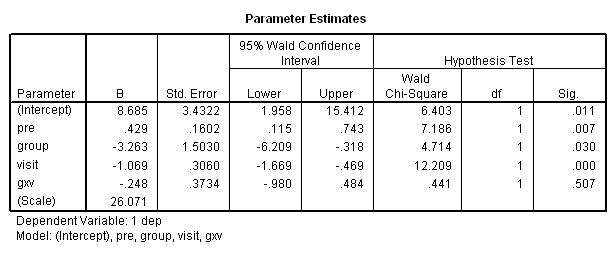
از طرفی دیده می‌شود که در تحلیل داده پانلی شاخص انحراف استاندارد برای ضرایب مدل نیز نسبت به مدل قبلی، افزایش داده است. بنابراین مدل حاصل، یک مدل بهینه نخواهد بود.

تحلیل داده پانلی با در نظر گرفتن متغیر ترتیبی

این بار می‌خواهیم متغیر visit را به صورت یک متغیر دو وضعیتی درآورده و ساختار داده‌ها را تغییر دهیم. به این ترتیب چندین متغیر مثل visit2 تا visit6 خواهیم داشت که با ۰ و ۱ مقدار دهی شده‌اند. میزان افسردگی به عنوان متغیر وابسته نیز در dep قرار گرفته است. این کار درست به مانند ایجاد یک مدل رگرسیونی با «متغیرهای مجازی» (Dummy Variable) است.

کد زیر به منظور ایجاد متغیرهای دو وضعیتی نوشته شده. در انتها نیز مدل GEE به کار گرفته و خروجی‌ها درخواست شده‌اند.

compute visit2 = ۰.
if visit = ۲ visit2 = ۱.
compute visit3 = ۰.
if visit = ۳ visit3 = ۱.
compute visit4 = ۰.
if visit = ۴ visit4 = ۱.
compute visit5 = ۰.
if visit = ۵ visit5 = ۱.
compute visit6 = ۰.
if visit = ۶ visit6 = ۱.
exe.
genlin dep with pre visit2 visit3 visit4 visit5 visit6 group 
 /model pre visit2 visit3 visit4 visit5 visit6 group distribution = normal link = identity
 /repeated subject = subj corrtype = ar(۱).

در تصویر ۲۳، نتایج حاصل برای پارامترها را مشاهده می‌کنید. مشخص است که ضریب‌ها در زمانی که به visit6 می‌رسیم، از لحاظ مقدار منفی، کوچکتر شده و نشانگر رابطه معکوس با میزان افسردگی هستند. به جز متغیر visit2، همگی متغبرهای طبقه‌ای در سطح ۰٫۰۵ از لحاظ آماری معنی‌دار شده‌اند.

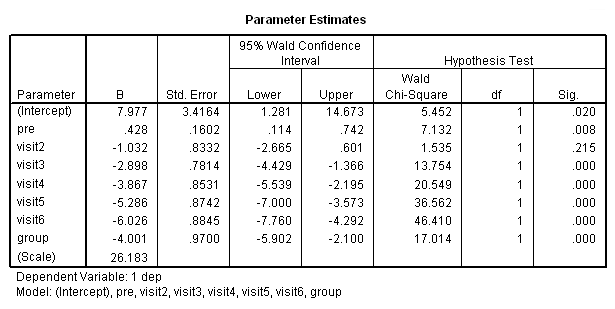
این بار سعی می‌کنیم مدل GEE با ساختار اتورگرسیو را برای متغیرهای visit (به عنوان یک متغیر پیوسته) و بقیه متغیرها دو وضعیتی (به جز متغیر visit6) به کار بگیریم. واضح است که اثر visit6‌ در متغیر visit نهفته است. به کد زیر دقت کنید.

genlin dep with pre visit visit2 visit3 visit4 visit5 group 
 /model pre visit visit2 visit3 visit4 visit5 group distribution = normal link = identity
 /repeated subject = subj corrtype = ar(۱).

در تصویر ۲۴، برآورد پارامترها دیده می‌شود که مشخص است نتوانسته، برتری نسبت به مدل قبلی ارائه دهد. بیشتر متغیرها یعنی visit2 تا visit5، معنی دار نبوده و بی‌اثر تشخص داده شده‌اند.

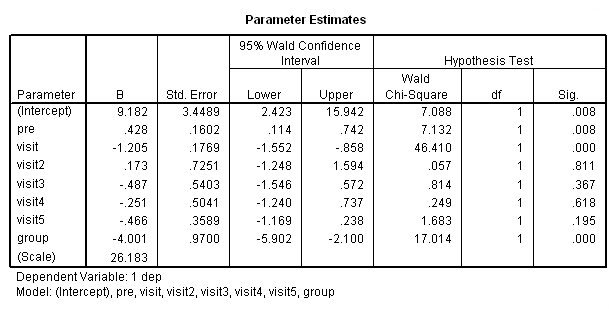
در نتیجه تغییر متغیر به صورت طبقه‌ای یا متغیرهای مجازی، نتوانسته است نسبت به حالت اصلی متغیر visit، در برآوردها اثر بخش باشد. پس متغیر گروه‌بندی visit که به صورت گسسته درآمده نتوانسته است نسبت به نسخه پیوسته آن تغییر محسوسی ایجاد کند. در آخرین بخش مدل را با استفاده از متغیرهای visit و group به همراه pre ساخته و متغیر dep را وابسته در نظر می‌گیریم.

genlin dep with pre visit group
 /model pre group visit distribution = normal link = identity
 /repeated subject = subj corrtype = ar(۱).

اجرای این قطعه کد، پارامترها را مطابق با جدول تصویر ۲۵، برآورد کرده است.

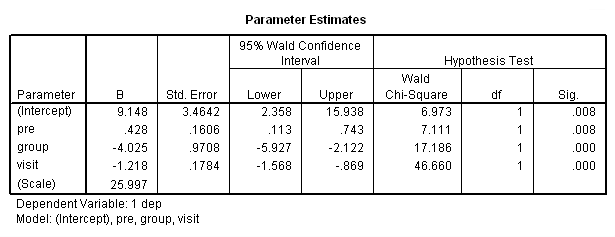
تفسیر نهایی این نتایج نشان می‌دهد که هر سه متغیر، اثر قابل توجه برای پیش مدل دارند. به عنوان مثال، به ازاء یک واحد افزایش در pre، با توجه به کنترل متغیرهای visit و group، میزان شاخص افسردگی، حدود ۰٫۴۲۸ واحد افزایش می‌یابد.

استفاده از داروی استروژن نیز با کنترل دو متغیر pre و group باعث کاهش شاخص افسردگی خواهد شد. مشخص است که استفاده از استروژن میزان شاخص افسردگی پس از زایمان را ۴ واحد کاهش می‌دهد که نشانه اثر بخش بودن این تیمار یا دارو محسوب می‌شود.

دوره اندازه‌گیری نیز موثر بوده و در هر دوره، به طور متوسط به میزان ۱٫۲، شاخص افسردگی کاهش می‌یابد. البته این امر به شرط ثابت بودن اثرات دو متغیر دیگر صورت گرفته است.

خلاصه و جمع‌بندی

در این نوشتار با نحوه اجرای تحلیل معادلات برآوردیابی تعمیم یافته یا به اختصار GEE در محیط نرم‌افزار SPSS آشنا شدید. همانطور که در نوشتارهای دیگر مجله ریسمونک خواندید، تحلیل داده پانلی با استفاده از تکنیک GEE که یک روش ناپارامتری است، شرایط کمتری داشته و با استفاده از تابع genlin‌ در SPSS‌ قابل اجرا است. البته تحلیل داده پانلی را به شیوه‌های دیگر مانند رگرسیون و آنالیز واریانس با مقادیر تکراری نیز انجام دادیم ولی شرایط مربوط به صحت این تکنیک‌ها، مشکل بوده و ممکن است محقق نشوند. بنابراین به عنوان یک روش جایگزین می‌توان از GEE که بدون توجه به توزیع یا فرضیه‌های دیگر اجرا می‌شود، محاسبه و برآورد پارامترها را انجام داد.

+ همچنین در ریسمونک بخوانید:

بهترین نرم افزار های رشته عمران چیست ؟