انحراف معیار به چه دردی میخورد؟
انحراف معیار مفهومی است که میزان پراکندگی دادههای یک مجموعه را مشخص میکند و بدین جهت یکی از مهمترین مقیاسهای آماری در زمینه آمار توصیفی به حساب میآید. اگر میانگین برآوردی از نقطه ثقل توزیع دادههای یک مجموعه به دست میدهد، و از این رو مقیاسی تکبعدی برای برآورد یک مجموعه دادهها فراهم میسازد، میتوان گفت که انحراف معیار نیز میزان پراکندگی دادهها از نقطه میانگین را نشان میدهد و از این رو مقیاسی دوبعدی برای برآورد توزیع دادهها در اختیار ما قرار میدهد.
مثال
برای مثال اگر یک معلم هستید، احتمالاً برایتان مهم است که بدانید دانشآموزان شما در امتحانی که اخیراً گرفتهاید چه عملکردی داشتهاند. اگر ۲۰ یا ۳۰ دانشآموز داشته باشید با نگاه کردن به تکتک نمرات شاید نتوانید برآورد صحیحی از عملکرد کل کلاس به دست آورید، ولی مسلماً در صورتی که میانگین نمرههای همه دانشآموزان را محاسبه کنید، میتوانید بدانید که وضعیت کل کلاس چگونه بوده است. برای مثال اگر میانگین نمرههای کلاس برابر با ۱۲٫۵ باشد و میانگین محاسبه شده برای امتحان قبلی ۱۴ بوده باشد، نشان دهنده افت نمرات است و نیاز به چارهجویی وجود دارد.
شما به عنوان یک معلم باید با کدام دانشآموزان بیشتر کار کنید؟ مسلماً برای دانشآموزانی که عملکرد بهتری دارند نیاز چندانی به تلاش بیشتر وجود ندارد، اما به دانشآموزانی که عملکرد ضعیفتری دارند میبایست توجه ویژهای صورت بگیرد. اما چگونه میتوان فهمید که کدام دانشآموزان عملکرد بالاتر دارند، متوسط هستند یا عملکرد ضعیفتری دارند؟ پاسخ به این سؤال از طریق محاسبه انحراف معیار است. انحراف معیار مقیاسی به دست میدهد که با استفاده از آن میتوانیم بدانیم میانگین اختلاف عملکرد دانشآموزان از نقطه میانگین کلاسی چقدر است.
برای مثال فرض کنید در کلاس شما انحراف معیار برابر با ۲٫۵ باشد. اگر توزیع نمرات دانشآموزان به صورت یک توزیع نرمال باشد (که در اغلب موارد در مورد چنین اندازهگیریهایی از توزیع نرمال پیروی میکند)، این عدد نشان میدهد که نمرات بیش از دو سوم یا ۶۸٫۲% از دانشآموزان شما در محدوده ۲٫۵ + ۱۲٫۵ قرار دارد. این عدد طبق تعریف انحراف معیار به دست میآید. یک سوم دیگر از دانشآموزان یا نمراتی بالاتر از ۱۵ کسب کردهاند که طبعاً نیاز چندانی به تلاش بیشتر شما ندارند و یا نمراتی زیر ۱۰ کسب کردهاند که مسلماً نیازمند توجه ویژه هستند. بدین ترتیب با محاسبه انحراف معیار نمرههای کلاسی میتوانید دانشآموزان را به سه دسته ضعیف (کمتر از ۱۰)، متوسط (۱۰ تا ۱۵) و قوی (بالاتر از ۱۵) تقسیمبندی کنید.
فرض کنید در مثال فوق تعداد دانشآموزانی که نمرات زیر ۱۰ کسب کرده بودند یعنی مردود بودند برابر با ۵ بوده است. همچنین فرض میکنیم معلم با این دسته از دانشآموزان تمرین میکند ولی در امتحان بعدی میانگین نمرات کلاس هنوز همان ۱۲٫۵ است. شاید در نگاه اول به نظر برسد، تلاشهای وی بینتیجه بوده است؛ اما با محاسبه انحراف معیار میبینیم که این عدد به ۱ کاهش یافته است، یعنی نمرات بیش از دوسوم کلاس در محدوده ۱ + ۱۲٫۵ قرار دارد. این به آن معنی است که به احتمال بسیار زیاد تعداد دانشآموزانی که نمره زیر ۱۰ کسب کردهاند، کاهش یافته است.
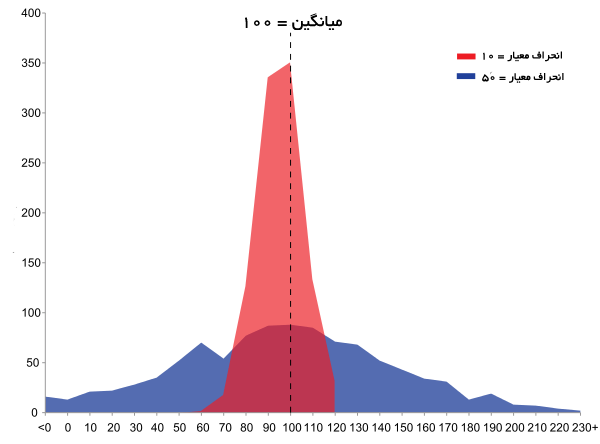
در تصویر فوق به خوبی اهمیت مفهوم انحراف معیار در برآورد توزیع دادهها را میبینید. هر دو مجموعه دادههای آبی و قرمز رنگ میانگینی برابر با ۱۰۰ دارند ولی انحراف معیار مجموعه دادههای آبی ۵ برابر دادههای قرمز است. علامتی که برای نشان دادن انحراف معیار استفاده میشود، حرف یونانی سیگما ” σ ” است. روشی که عموماً برای محاسبه انحراف معیار استفاده میشود از طریق جذر گرفتن از واریانس است. خب اکنون شاید بپرسید واریانس چیست؟
واریانس چیست؟
واریانس به صورت «مقدار متوسط مربع اختلاف مقادیر از میانگین» تعریف شده است. شاید در نگاه نخست تعریف دشواری به نظر برسد! اما هیچ جای نگرانی نیست چون در عمل خواهید دید که مفهوم بسیار سادهای است.
برای محاسبه واریانس، باید گامهای زیر را دنبال کنید:
- ابتدا میانگین را پیدا کنید (میانگین ساده اعداد).
سپس برای هر عدد، مقدار میانگین را از آن تفریق کرده و سپس نتیجه را به توان دو برسانید (مربع اختلاف).
و در نهایت میانگین مربع اختلافات به دست آمده را محاسبه کنید.
واریانس دادهها آماده است. به همین سادگی!
مثال
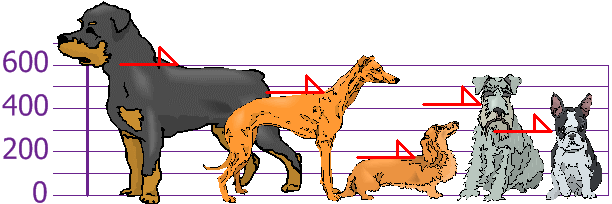
فرض کنید متصدی یک محل نگهداری از سگها میخواهد قد سگهای موجود را به منظور خاصی اندازهگیری کند. نتایج این اندازهگیری قد (از شانه) به شرح زیر است:
۳۰۰، ۴۳۰، ۱۷۰، ۴۷۰ و ۶۰۰ میلیمتر
اینک میخواهیم میانگین، واریانس و انحراف معیار این دادهها را پیدا کنیم. گام اول یافتن میانگین است: