استفاده از هوش مصنوعی در مسائل بهینه سازی ترکیباتی
مسائل «بهینه سازی ترکیباتی» (Combinatorial Optimization | CO)، دسته مهمی از مسائل محسوب میشوند که در آن، تعداد راهحلهای ممکن بهصورت ترکیبی با اندازه مسئله، افزایش مییابد. این نوع از مسائل، توجه بسیاری از پژوهشگران علوم کامپیوتر، پژوهشهای عملیاتی و «هوش مصنوعی» را به خود جلب کرده است. اصلیترین هدف «بهینه سازی ترکیباتی»، یافتن راهحلی «بهینه» (Optimal) یا «شِبه بهینه» (Near-Optimal) برای مسائل پیچیده است که این کار بهوسیله روشهای بهینهسازی گوناگون برای «کمینهکردن» (Minimize) هزینهها و «بیشینهکردن» سود و کارایی استفاده میشود.
بهینهسازی ترکیباتی، شاخهای از ریاضیات و علوم کامپیوتر بهشمار میرود که به دنبال پیدا کردن بهترین راهکار ممکن از مجموعه محدودی از راهحلهای ممکن است، یعنی زمانیکه با ترکیبهای ممکن متعددی رو به رو هستیم. این رویکرد، بهدلیل توانایی در حل مسائل پیچیده، در طیف وسیعی از کاربردهای موجود در صنایع گوناگون مورد استفاده قرار میگیرد.
برای حل مسائل بهینهسازی ترکیباتی به طور معمول از الگوریتمها و همچنین روشهای مختلفی کمک میگیریم و این مورد، به نوع مسئله و اندازه آن بستگی دارد. اگر بخواهیم یک نمای کلی از مراحل و چگونگی حل مسائل بهینهسازی ترکیباتی داشته باشیم، میتوانیم به مواردی که در ادامه فهرست شده، اشاره کنیم.
- تعریف مسئله
- فرمولهسازی ریاضی
- انتخاب الگوریتم
- پیادهسازی الگوریتم
- پیکربندی
- حل مسئله
- پسپردازش
- تکرار ۴ مرحله قبل (در صورت لزوم)
- ارزیابی راهحل
- عرضه نتایج به مشتریان
- استقرار
البته میبایست در نظر داشته باشیم که این مراحل، بیانگر حالت کلی هستند و بسته به خصوصیات مسئله مورد نظر، ممکن است الگوریتمها و روشهای متفاوتی را بهکار بگیریم.
میتوانیم بگوییم که بهینهسازی ترکیباتی، ابزار نیرومندی برای حل مسائل پیچیده موجود در حوزههای گوناگون محسوب میشود که در آن، فرایند تصمیمگیری شامل انتخاب بهترین ترکیب عناصر، از مجموعه بزرگی از احتمالات است. همچنین به بهبود کارایی، کاهش هزینهها، افزایش کیفیت و حل چالشهای مربوط به تخصیص منابع در طیف گستردهای از برنامهها کمک میکند.
درس سیستم عامل در مقطع کارشناسی
بهینه سازی ترکیباتی چیست؟
«بهینه سازی ترکیباتی» (Combinatorial Optimization)، زیرشاخهای از حوزه «بهینهسازی ریاضی» محسوب میشود که بهدنبال پیدا کردن «شی بهینه» (Optimal Object) از مجموعه محدودی از اشیا است. مجموعه راهحلهای عملی یا «ممکن» (Feasible)، «گسسته» (Discrete) هستند یا میتوان آن را به مجموعهای گسسته تقلیل داد.
از مسائل بهینه سازی ترکیباتی، میتوان به «مسئله فروشنده دوره گرد» (Travelling Salesman Problem | TSP)، مسئله «درخت پوشای کمینه» ( Minimum Spanning Tree | MST) و «مسئله کولهپشتی» (Knapsack Problem) اشاره کرد. در بسیاری از اینگونه مسائل، نمیتوانیم از جستوی کامل یا «برات فورس» (Brute-Force Search) برای حل مسئله استفاده کنیم. بنابراین بهجای آن، از الگوریتمهایی که بهسرعت، بخشهای بزرگی از فضای جستجو را نادیده میگیرند و همچنین از «الگوریتمهای تقریبی» (Approximation Algorithms) کمک میگیریم.
از مباحث مرتبط با «بهینه سازی ترکیباتی»، میتوان به «تحقیق در عملیات» (Operations Research)، «نظریه الگوریتم» (Algorithm Theory) و «نظریه پیچیدگی محاسباتی» (Computational Complexity Theory) اشاره کرد.
برخی از آثار پژوهشی، «بهینهسازی گسسته» (Discrete Optimization) را در برگیرنده «برنامهنویسی عدد صحیح» (Integer Programming) بههمراه بهینهسازی ترکیباتی – که از مسائل بهینهسازی مربوط به گرافها تشکیل شده است – میدانند. تمامی این مباحث در پژوهشها، ارتباط تنگاتنگی با هم دارند و بهدنبال روشی برای تخصیصِ کارآمد منابع، به منظور کشف راهحلهایی برای مسائل ریاضی هستند.
«مسائل بهینهسازی ترکیباتی» (Combinatorial Optimization Problems | COP) را میتوان فرایندی در نظر گرفت که به منظور کشف راهکار بهینه از طریق ارزیابی تعداد محدود و ثابتی از ترکیبات انجام میشود. در بیشتر موارد، اینگونه مسائل با تئوری گراف یا «برنامهریزی خطی» (Linear Programming) مدل میشوند.
مسائل بهینهسازی ترکیباتی در کاربردهای مختلفی همچون تحویل کالا به مشتریان، یافتن کوتاهترین مسیر، تخصیص وظایف به کارمندان و غیره ظاهر میشوند و با کاهش هزینه و زمانِ صرف شده، به ما کمک میکنند تا بهرهوری را افزایش دهیم.
کاربرد بهینهسازی ترکیباتی چیست؟
بهینه سازی ترکیباتی به منظور حل مسائل موجود در حوزههای گوناگونی که در ادامه فهرست کردهایم، مورد استفاده قرار میگیرند.
- هوش مصنوعی
- «یادگیری ماشین» (Machine Learning)
- «نظریه مزایده» (Auction Theory)
- مهندسی نرمافزار
- «یکپارچهسازی کلان مقیاس» (Very-Large-Scale Integration | VLSI)
- ریاضیات کاربردی
- «علوم نظری کامپیوتر» (Theoretical Computer Science)
از کاربردهای موضوعیِ بهینهسازی ترکیباتی همچنین میتوان به موارد فهرست شده در زیر اشاره کرد.
- لجستیک یا «تدارکات» (Logistics)
- «بهینه سازی زنجیره تأمین» (Supply Chain Optimization)
- ایجاد بهترین شبکه خطوط هوایی با استفاده از مسیرها و مقاصد موجود
- تعیین روشی بهینه برای تحویل بستهها
- تخصیص بهینه مشاغل به افراد
- طراحی شبکههای توزیع آب
مثال هایی از مسائل بهینه سازی ترکیباتی
در ادامه، چندین مدل که برای سادهسازی و فرمولهکردن مسائل دنیای واقعی استفاده میشوند را بیان کردهایم.
- «درخت پوشای کمینه» (Minimum Spanning Tree Problem | MST): با در نظر گرفتن گرافی متصل و بدون جهت بهنام
، درخت پوشا را میتوان زیرگرافی از
- در نظر گرفت که تمامی رأسها را به هم وصل میکند. وزن MST، کمتر یا مساوی با وزن هر درخت پوشای دیگری است.
- «مسئله فروشنده دوره گرد» (Travelling Salesman Problem | TSP): با اینکه «فروشنده دوره گرد» مسئلهای کلاسیک بهشمار میرود با این حال هنوز هم در ریاضیات، «تحقیق در عملیات» و «بهینهسازی» رایج است.
- «مسئله کوله پشتی» (Knapsack Problem): این مسئله، بیشتر بههنگام «تخصیص منابع» (Resource Allocation) رخ میدهد که در آن «محدودیتهای مالی» (Financial Constraints) وجود دارد. مسئله «کوله پشتی» همچنین در حوزههایی نظیر علوم کامپیوتر، نظریه پیچیدگی، «رمزنگاری» (Cryptography) و ریاضیات کاربردی نیز مورد مطالعه قرار میگیرد.
حل مسئله فروشنده دوره گرد
مسئله اصلی، فروشنده دورهگردی را معرفی میکند که میبایست از چندین شهر بازدید کند. سوال و مسئلهای که در اینجا وجود دارد این است که برای انجام کوتاهترین سفر ممکن، ترتیب بازدید از شهرها به چه صورتی باید باشد. لازم به ذکر است که فروشنده میبایست تمامی شهرها را یک مرتبه بازدید کند و در نهایت به موقعیت اولیه بازگردد. در ادامه، مدل ریاضی مسئله TSP را آوردهایم.

تعریف رسمی مسئله فروشنده دوره گرد
بهطور معمول برای مدل کردن مسئله TSP از گراف
کمک میگیریم. با ، مجموعهای از رئوس است که هر کدام شهری را نشان میدهد، در حالیکه
مجموعهای از یالها را نشان میدهد که بیانگر فاصله بین هر جفت از شهرها هستند.
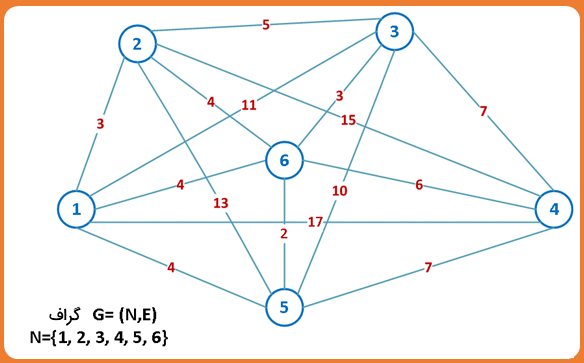
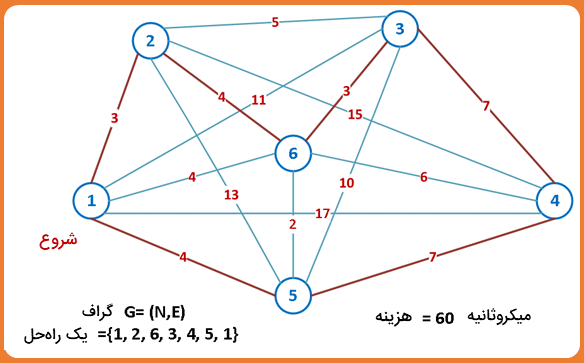
یک نمونه «TSP» با اندازهای نسبتاً کوچک
میگیریم. فرض میکنیم که کامپیوتر برای محاسبه هر راهحل به یک واحد زمانی احتیاج دارد. (یک میکروثانیه در هر مسیر).
برای بررسی هر یک از راهحلهای ممکن و انتخاب بهترینِ آن، نیاز داریم تا راهحل ممکن (راهحل نامزد) را محاسبه کنیم. در مثال ما این مقدار برابر است با
که یعنی محاسبات آن ۶۰ میکروثانیه طول میکشد.
با این حال، اگر فرض کنیم که
باشد، در این صورت کاوش در فضای جستجو چیزی در حدود ۱۹ قرن طول خواهد کشید. واضح است که این مقدار زمانی بسیار زیاد است. جدولی که در ادامه آوردهایم، مدت زمان لازم برای محاسبه تعداد مسیرهای ممکن با توجه به تعداد شهرها را نشان میدهد.
| تعداد شهرها | تعداد مسیرهای ممکن | زمان محاسباتی |
| ۵ | ۱۲ | ۱۲ میکروثانیه |
| ۱۰ | ۱۸۱۴۴۰ | ۰٫۱۸ ثانیه |
| ۱۵ | ۴۳ میلیارد | ۱۲ ساعت |
| ۲۰ | ۶E+16 | ۱۹ قرن |
| ۲۵ | ۳E+23 | ۹٫۸ میلیارد سال |
| ۳۰ | ۴E+30 | ۱٫۴ میلیون میلیارد قرن |
راه حل های بهینه سازی ترکیباتی
همانگونه که در مثال TSP دیدیم، این مسائل همیشه به آسانی حل نمیشوند. تعداد راهحلهای ممکن معمولاً بسیار زیاد است و نیاز به «جستجوی کامل» (Exhaustive Search) در فضای راه حل دارد. به همین دلیل است که COP-ها از نظر محاسباتی پرهزینه هستند. این مسائل به دسته مسائل «NP-hard» تعلق دارند. هدفی که ما بهدنبال آن هستیم، این است که راهحلی «نزدیک به بهینه» (Near-Optimal) را در مدت زمانی معقول پیدا کنیم.
۲ رویکرد اصلی برای حل این نوع مسائل را در ادامه آوردهایم.
- «راهحلهای دقیق» (Exact Solutions): این نوع راهحلها دستیابی به «بهینه سراسری» (Global Optimum) را تضمین میکنند. با این وجود، رسیدن به نتایج بسیار زمانبر است و همچنین هزینههای پیچیدگی بالایی بهدنبال دارد. بهبیان دیگر تنها برای مسائل کوچک مناسب هستند. برای نمونه میتوان به الگوریتمهای «شاخه و کران» (Branch and bound) و «برنامهنویسی پویا» (Dynamic programming) اشاره کرد.
- «راهحلهای تقریبی» (Approximative Solutions): این راهحلها بر «Trade-Off» متکیاند. راهحلی تقریبی پیدا میکنند و در عین حال بسیار سریع هستند. بهکمک این روش میتوانیم به حل مسائل بزرگ بپردازیم. این روشها در کل، به دو دسته اصلی «ابتکاری» (Heuristics) و «فرا ابتکاری» (Metaheuristic) خاصِ مسئله، تقسیم میشوند.

روش های بهینه سازی ترکیباتی چیست؟
پژوهشهای زیادی در مورد «الگوریتمهای زمانی چندجملهای» (Polynomial-Time Algorithms) برای طبقات خاصی از بهینهسازی گسسته وجود دارد. مقدار قابل توجهی از آن توسط نظریه «برنامهریزی خطی» (Linear Programming) منسجم شده است. برخی از نمونههای مسائل «بهینهسازی ترکیبی» که توسط این چارچوب پوشش داده میشوند، در ادامه فهرست شده است.
- «کوتاهترین مسیر» (Shortest-Path) و «درختهای کوتاهترین مسیر» (Shortest Paths Trees)
- «شبکه شاره» (Flow Network)
- «درختهای پوشا» (Spanning Trees)
- «تطابق » (Matching) در گراف
- مسائل «مِیتروید» (Matroid)
برای مسائل بهینهسازی گسسته «اِن پی کامل» (NP-complete)، ادبیات پژوهشی کنونی، موضوعاتی که در ادامه آمده است را در بر میگیرد.
- موارد خاصی از مسئله که دقیقاً در «زمان چندجملهای» (Polynomial-Time)، قابل حل است. بهطور مثال میتوان به مسائل قابلِ حل با «پارامتر ثابت» یا «Fixed-Parameter Tractable» اشاره کرد.
- الگوریتمهایی که روی نمونههای تصادفی، بهخوبی عمل میکنند (بهعنوان مثال برای مسئله فروشنده دوره گرد).
- «الگوریتمهای تقریبی»، که در «زمان چندجملهای» اجرا میشوند و راهحلی نزدیک به بهینه را کشف میکنند.
- «الگوریتمهای تقریبی پارامتری» (Parameterized Approximation Algorithms) که در زمان «FPT» اجرا میشوند و راهحلی نزدیک به بهینه (شبه بهینه) پیدا میکنند.
- حل نمونههای واقعی که در عمل رخ میدهند و لزوماً بدترین رفتار را در مسائل NP-کامل نشان نمیدهند (بهعنوان مثال نمونههای TSP واقعی با هزاران گره).

مسائل بهینهسازی ترکیبی را میتوان بهعنوان جستجوی بهترین عنصر در مجموعهای از موارد گسسته در نظر گرفت. بنابراین، از هر نوع «الگوریتم جستجو» (Search Algorithm) یا «فرا ابتکاری» (Metaheuristic) میتوان برای حل آنها استفاده کرد. احتمالاً کاربردیترین رویکردها در سطح عمومی شامل مواردی است که در ادامه آوردهایم.
- «شاخه و کران» (Branch-and-Bound): الگوریتمی دقیق که میتوان آن را در هر نقطه از زمان متوقف کرد تا بهصورت اکتشافی عمل کند.
- «شاخه و برش» (Branch-and-Cut): الگوریتمی که از بهینهسازی خطی برای تولید کران استفاده میکند.
- «برنامهنویسی پویا» (Dynamic Programming): راهحل بازگشتی با پنجره جستجوی محدود.
- «جستجوی ممنوعه» (Tabu Search): الگوریتمی مبادلهای یا تعویضی از نوع حریصانه.
با این حال، الگوریتمهای عمومی جستجو تضمین نمیکنند که در ابتدا، راهحل بهینهای را پیدا کنند. همچنین تضمینی برای اجرای سریع آنها (در زمان چند جملهای) وجود ندارد. از آنجاییکه برخی از مسائل بهینهسازی گسسته، «NP-کامل» هستند، مانند مسئله فروشنده دوره گرد (تصمیم گیری)، این امر طبیعی است مگر اینکه P=NP باشد.
تعریف صوری
مسئله «بهینهسازی ترکیبی A» را در نظر میگیریم، این مسئله بهصورت یک ۴ تایی به شکل
که جزئیات آن را در ادامه آوردهایم، تعریف میشود.
- بیانگر مجموعهای از نمونهها است.
- با توجه به
، تابع
- ، مجموعهای متناهی از راهحلهای ممکن است.
- با توجه به نمونه
و راهحل ممکن از ، اندازه
- را نشان میدهد که معمولاً مثبت حقیقی است.
- بیانگر تابع هدف است که میتواند «min» یا «max» باشد.
هدف، این است که برای برخی از نمونههای
«راهحلی بهینه» پیدا کنیم، که «راهحل ممکن»
بهصورت زیر است.
برای هر مسئله «بهینه سازی ترکیباتی»، یک «مسئله تصمیم» (Decision Problem) متناظر با آن وجود دارد و این پرسش را در نظر دارد که آیا «راهحل ممکن» (Feasible Solution) برای مقدار خاصی از
وجود دارد یا خیر. برای مثال، اگر گراف که شامل رئوس و است را در نظر بگیریم، مسئله بهینهسازی، ممکن است بهصورت «یافتن مسیری از به با حداقل تعداد یال» تعریف شود. این مسئله میتواند پاسخی مانند «۴» داشته باشد. حال اگر «مسئله تصمیم» متناظر با آن را در نظر بگیریم، میتواند به این صورت باشد که آیا مسیری از رأس به رأس
که شامل ۱۰ یال یا کمتر باشد وجود دارد یا خیر». این مسئله نیز میتواند پاسخی ساده مانند «بله» یا «خیر» داشته باشد.

حوزه «الگوریتمهای تقریبی» (Approximation Algorithms)، با الگوریتمهایی سروکار دارد که به یافتن راهحلهای «نزدیک به بهینه» (Near Optimal) برای حل مسائل سخت میپردازند. نسخه تصمیمگیری رایج (اشاره به مسئله تصمیم)، تعریفی ناکافی از مسئله ارائه میدهد، چون تنها راهحلهای قابل قبول (مناسب) را مشخص و بیان میکند. اگرچه میتوانیم «مسائل تصمیم» (Decision problem) مناسبی را معرفی کنیم، اما بهتر است که مسئله، بهعنوان «مسئله بهینهسازی» توصیف شود.
مسائل بهینه سازی NP چیست؟
«مسئله بهینه سازی اِنپی» (NP-Optimization Problem | NPO)، مسئله «بهینه سازی ترکیباتی» است که شرایط زیر را نیز در بر میگیرد.
- اندازه هر «راهحل ممکن»
، چند جملهای «کراندار»، به اندازه نمونه داده شده
- است.
- زبان
و
- ، در زمان چندجملهای مشخص میشود.
- و
- نیز در زمان چندجملهای قابل محاسبه است.
این قضیه، بیانگر این است که «مسئله تصمیمِ» متناظر، از نوعِ «NP» است. در علوم کامپیوتر، مسائل بهینهسازی محبوب، معمولاً ویژگیهای بیان شده را دارند و بههمین دلیل مسائل «NPO» بهشمار میروند. همچنین، اگر الگوریتمی وجود داشته باشد که راهحلهای بهینه را در زمان چندجملهای پیدا کند، «مسئله بهینهسازیِ پی» (P-Optimization | PO) نامیده میشود. خیلی وقتها، هنگام کار با «NPO»، افراد بر روی نوعی از مسائل بهینهسازی تمرکز میکنند که در آن نسخههای تصمیم «NP-Complete» هستند.
سوالات متداول
در این قسمت به بیان برخی از سوالات رایج در مورد اینکه بهینه سازی ترکیبی چیست و همچنین پاسخ متناظر آنها پرداختهایم.
معروف ترین مسائل بهینه سازی ترکیباتی چیست؟
از متداولترین مسائل بهینه سازی ترکیباتی میتوان به «مسئله فروشنده دوره گرد» (Travelling Salesman Problem | TSP)، «درخت پوشای کمینه» (Minimum Spanning Tree Problem | MST) و مسئله «کوله پشتی» (Knapsack Problem) اشاره کرد.
در بهینه سازی ترکیبی چه چیزی را بهینه می کنیم؟
بهینه سازی ترکیباتی، فرایندی است که در آن به دنبال «بیشینه» (Maxima) یا «کمینه» (Minima) یک «تابع هدف» (Objective Function) مانند F میگردیم که دامنه آن، فضای پیکربندی گسسته اما بسیار بزرگ است (درست برخلاف فضای پیوسته N بُعدی).
ویژگی های کلیدی مسئله در بهینه سازی ترکیباتی چیست؟
مسائل بهینه سازی ترکیباتی شامل یافتن «گروهبندی» (Grouping)، «ترتیببندی» (Ordering) یا «تخصیص» (Assignment) مجموعه گسسته و محدودی از اشیا است که شرایط داده شده را برآورده میکند. راهحلهای کاندید (ممکن)، ترکیبی از اجزای راهحل هستند که ممکن است در طول تلاش برای یافتن راهحل، با آنها مواجه شویم، اما نیازی به برآورده کردن تمامی شرایط داده شده ندارند.
میزان دشواری بهینه سازی ترکیباتی چقدر است؟
از بین تعدادی محدود یا نامحدود از گزینههای شمارش پذیر، نیاز داریم که بهترین راهحل را بر اساس معیار قابل اندازهگیری، انتخاب کنیم. خیلی از مسائل شناخته شده بهینهسازی ترکیباتی، در دسته مسائل «NP-سخت» (NP-hard) قرار دارند و محاسبات بسیار سخت دارند.
اهمیت بهینه سازی ترکیباتی چیست؟
بهینه سازی ترکیباتی اساساً برای حل مسائل بهینهسازی گسسته با بهکارگیری روشهای ترکیباتی، مورد استفاده قرار میگیرد. مسائل بهینهسازی گسسته در اصل مسائلی هستند که به کشف بهترین راه حل ممکن از مجموعه محدودی از احتمالات میپردازند.
جمعبندی
در این مطلب از مجله فرادرس، توضیح دادیم که بهینه سازی ترکیباتی چیست و همچنین ویژگیها و کاربردهای آن را نیز بیان کردیم.
از منظر علوم کامپیوتر، بهینه سازی ترکیباتی با بهکارگیری روشهای ریاضی بهدنبال بهبود یک الگوریتم است و این امر با کاهش اندازه مجموعه جوابهای ممکن یا افزایش سرعت جستجو انجام میشود.