محیط دایره برابر با حاصلضرب قطر (دو برابر شعاع) در عدد پی (عدد ثابت ۳/۱۴) است. محیط دایره، با استفاده از اندازه شعاع یا قطر به دست میآید. البته حالتهای مختلفی برای محاسبه محیط وجود دارند. در این آموزش، ضمن تعریف محیط دایره و فرمولهای محاسبه آن، چندین تمرین و مثال کاربردی و متنوع را حل میکنیم.
دایره چیست؟
دایره (به انگلیسی Circle)، از اشکال پایه هندسی است که از یک منحنی بسته تشکیل میشود. تمام نقاط موجود بر روی این منحنی، در فاصله مشخصی از یک نقطه ثابت قرار دارند.
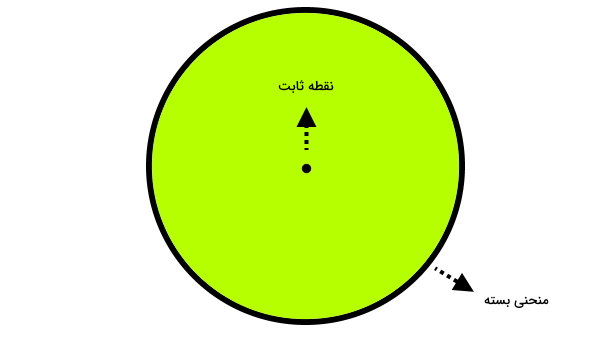
اجزای دایره چه هستند؟
مرکز، شعاع و قطر، از اجزای اصلی دایره هستند. برخلاف دیگر شکلهای هندسی پایه (مربع و مثلث)، دایره، هیچ ضلع، لبه و یا گوشهای ندارد.
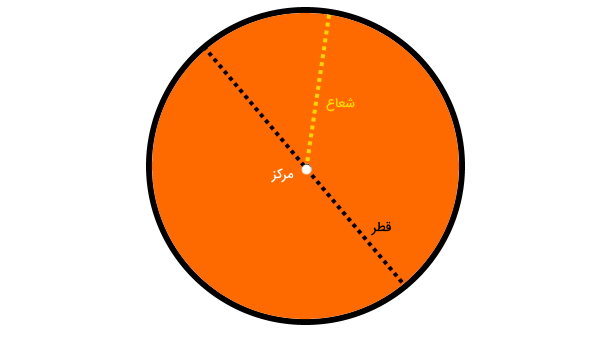
- مرکز: مرکز دایره، نقطهای است که تمام نقاط دایره، از آن به یک اندازه فاصله دارند.
- شعاع: فاصله بین نقاط دایره تا مرکز، با عنوان شعاع دایره شناخته میشود.
- قطر: قطر دایره، پارهخطی است که از مرکز دایره میگذرد و آن را به دو بخش مساوی تقسیم میکند. اندازه قطر دایره، دو برابر اندازه شعاع آن است.
محیط چیست؟
محیط، مسیر بستهای است که اندازه خطوط یا منحنیهای تشکیل دهنده یک شکل هندسی دو بعدی را نمایش میدهد. در چند ضلعیها، محیط، از جمع اندازه تمام ضلعها به دست میآید. تصویر زیر، محیط مربع را نمایش میدهد.

محیط دایره چیست ؟
محیط دایره (به انگلیسی Circumference)، اندازه مسیر منحنی تشکیل دهنده این شکل هندسی است. برای درک مفهوم محیط دایره، تصویر زیر را در نظر بگیرید. اگر یک قلم را بر روی نقطه ۱ قرار داده و آن را بر روی دایره در جهت ساعتگرد حرکت دهیم، پس از برگشتن به نقطه ۱، قلم، مسیر خط چین نمایش داده شده در تصویر زیر را طی میکند. این مسیر، همان محیط دایره است.
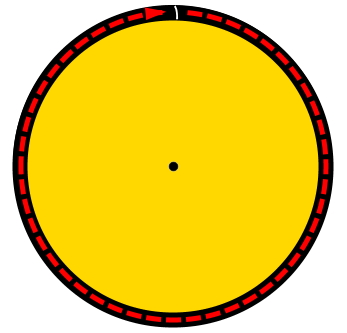
محیط دایره چگونه بدست می آید ؟
محیط دایره، از ضرب قطر در عدد پی (۳/۱۴) به دست میآید. البته محیط دایره با ضرب دو برابر شعاع در عدد پی نیز محاسبه میشود.
عدد پی چیست ؟
نسبت محیط هر دایره به قطر آن، تقریبا برابر ۳/۱۴ است. به این عدد ثابت، عدد پی میگویند. علامت عدد پی در فرمولهای ریاضی، با حرف یونانی π نمایش داده میشود.
مثال: تعیین محیط یک حوض دایرهای شکل
یک حوض به شکل دایره و با شعاع ۱/۵ متر را در نظر بگیرید. محیط این حوض چقدر است؟

در بخش قبلی، گفتیم که محیط دایره از رابطه زیر به دست میآید:
شعاع $$times$$ عدد پی $$times$$ 2 = محیط دایره
شعاع حوض برابر ۱٫۵ متر و عدد پی برابر ۳/۱۴ است. برای محاسبه محیط حوض دایرهای شکل، این اندازهها را در رابطه بالا قرار میدهیم:
۱٫۵ $$times$$ 3/14 $$times$$ 2 = محیط حوض
۱٫۵ $$times$$ 6.28 = محیط حوض
۹٫۴۲ = محیط حوض
در نتیجه، محیط حوض برابر ۹٫۴۲ متر است. این عدد، در اندازهگیری تعداد آجرهای مورد نیاز برای ساخت یک حوض مشابه، تغییر اطراف حوض و غیره کاربرد دارد.
محیط دایره با چه علامتی نمایش داده میشود؟
علامت جبری محیط دایره در فرمولهای ریاضی، حرف C، ابتدای کلمه انگلیسی «Circumference»، است. البته برای نمایش محیط شکلهای چند ضلعی مانند مربع، مستطیل، مثلث و غیره، معمولا از حرف انگلیسی P، ابتدای کلمه «Perimeter»، استفاده میشود.
فرمول محیط دایره چیست؟
پرکاربردترین و شناخته شدهترین فرمول محیط دایره، C=2πr است. هر یک از علامتهای این فرمول عبارت هستند از:
- C: محیط دایره
- π: عدد ثابت پی برابر ۳/۱۴
- r: شعاع دایره (نصف قطر) و ابتدای کلمه انگلیسی «radius» به معنای «شعاع»
در برخی از مسائل، برای ساده کردن محاسبات، عدد پی برابر ۳ در نظر گرفته میشود.
فرمول محیط دایره با قطر
به دلیل رابطه مستقیم بین شعاع و قطر دایره، فرمول اصلی محیط دایره را میتوان به صورت زیر بازنویسی کرد:
$$
C = pi d
$$
- C: محیط
- π: عدد ثابت برابر ۳/۱۴
- d: قطر دایره (دو برابر شعاع) و ابتدای کلمه انگلیسی «diameter» به معنای قطر
فرمول محیط دایره با مساحت
مساحت دایره، سطح محدود به محیط آن است. در صورت مشخص بودن مساحت دایره، محیط آن از فرمول زیر به دست میآید:
$$
C=2 sqrt{pi A}
$$
- C: محیط
- A: مساحت دایره
- π: عدد ثابت برابر ۳/۱۴
فرمول محیط قطاع دایره با زاویه
به هر بخش از محیط دایره، یک کمان گفته میشود. اگر دو طرف هر کمان را توسط شعاع به مرکز دایره وصل کنیم، یک قطاع به وجود میآید.
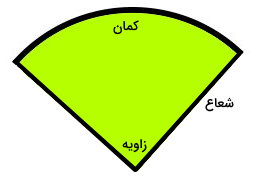
فرمول محاسبه اندازه کمان دایره بر حسب زاویه مقابل کمان برابر است با:
$$
l = r theta
$$
- l: طول کمان
- r: شعاع دایره
- θ: زاویه رو به روی کمان بر حسب رادیان
در اغلب موارد، زاویه مقابل کمان بر حسب درجه بیان میشود. به همین خاطر، برای حل فرمول بالا، ابتدا باید زاویه را با استفاده از رابطه زیر به واحد رادیان تبدیل کرد:
$$
rad = frac { deg times pi } {180}
$$
- rad: زاویه بر حسب رادیان
- deg: زاویه بر حسب درجه
- π: عدد ثابت ۳/۱۴
دو طرف کمان، توسط دو شعاع به مرکز دایره وصل شدهاند. از اینرو، با اضافه کردن اندازه این دو شعاع به طول کمان، محیط قطاع به دست میآید:
$$
C_{ s } = l_{ a } + 2r
$$
یا
$$
C_{ s } = l_{ a } + d
$$
- Cs: محیط قطاع دایره
- la: طول کمان
- r: شعاع دایره
- d: قطر دایره
فرمول محیط نیم دایره، ثلث دایره و ربع دایره
نیم یا یک دوم دایره، ثلث یا یک سوم دایره و ربع یا یک چهارم دایره، از انواع قطاعهای شناخته شده و پرکاربرد دایره هستند. بنابراین، محیط این شکلها، با استفاده از فرمول قطاع به دست میآید. البته برای محاسبه طول کمان در این قطاعها، نیازی به نوشتن فرمول بر حسب زاویه نیست.
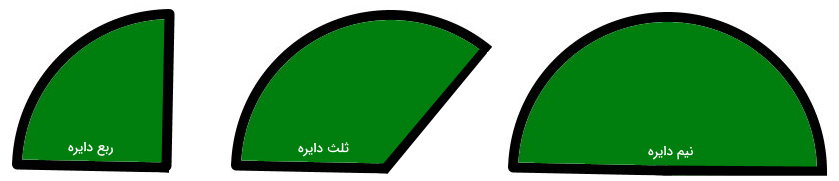
طول کمان نیمدایره، ثلث دایره و ربع دایره، نسبتی از محیط کل دایره است. از اینرو، طول کمان در فرمول محیط آنها، به صورت کسری از محیط کل نوشته میشود. به عنوان مثال، طول کمان نیمدایره، نصف محیط دایره کامل است.
جدول فرمول های محیط دایره
در این بخش و پیش از رفتن به بخش مثالها، فرمولهای محیط دایره و برخی از شکلهای هندسی مرتبط را در قالب یک جدول ارائه میکنیم.
| شکل هندسی | اندازه مورد نیاز | فرمول محیط |
| دایره | شعاع (r) | $$ C = 2 pi r $$ |
| دایره | قطر (d) | $$ C = pi d $$ |
| دایره | مساحت (A) | $$ C=2 sqrt{pi A} $$ |
| قطاع دایره | زاویه مقابل کمان (θ) | $$ C_{ s } = l_{ a } + 2r $$ , $$ l_a = r theta $$ |
| نیمدایره | شعاع (r) یا قطر (d) | $$ C_{ 1/2 } = frac {C} {2} + 2r $$ , $$ C_{ 1/2 } = frac {C} {2} + d $$ |
| ثلث دایره | شعاع (r) | $$ C_{ 1/3 } = frac {C} {3} + 2r $$ |
| ربع دایره | شعاع (r) | $$ C_{ 1/4 } = frac {C} {4} + 2r $$ |
| محیط مربع | ضلع (a) | $$ P = 4a $$ |
| محیط مثلث | ضلع اول (a)، ضلع دوم (b) و ضلع سوم (c) | $$ P = a + b+ c $$ |
مثال های محیط دایره
در این بخش، به حل چندین مثال متنوع و کاربردی در زمینه محاسبه محیط دایرهها، نیمدایرهها و شکلهای ترکیبی با دایره میپردازیم.
مثال اول: مقایسه محیط دایرهها
محیط دایرهای با شعاع ۴ سانتیمتر و دایرهای با قطر ۴ سانتیمتر را حساب کنید.
برای محاسبه محیط دایرهای با شعاع ۴ سانتیمتر از فرمول زیر استفاده میکنیم:
شعاع $$times$$ عدد پی $$times$$ 2 = محیط دایره
$$
C_r=2πr
$$
- Cr: محیط دایره
- π: عدد ثابت ۳/۱۴
- r: شعاع دایره برابر ۴ سانتیمتر
با جایگذاری اندازههای معلوم در فرمول بالا، خواهیم داشت:
$$
C_r=2 times 3/14 times 4
$$
$$
C_r= 6.28 times 4
$$
$$
C_r= 25.12
$$
فیلمهای آموزشی مرتبط
محیط دایرهای با شعاع ۴ سانتیمتر، برابر ۲۵/۱۲ سانتیمتر است. در مرحله بعد، برای محاسبه محیط دایرهای با قطر ۴ سانتیمتر، فرمول زیر را مینویسیم:
قطر $$times$$ عدد پی = محیط دایره
$$
C_d=πd
$$
- Cd: محیط
- π: عدد ثابت برابر ۳/۱۴
- d: قطر دایره برابر ۴ سانتیمتر
$$
C_d=3/14times 4
$$
$$
C_d=12.56
$$
محیط دایرههای با قطر ۴ سانتیمتر، برابر ۱۲٫۵۶ است. دقت کنید که در این دایره، شعاع برابر با ۲ سانتیمتر بود. در واقع، با نصف شدن شعاع، محیط نیز (از ۲۵٫۱۲ به ۱۲٫۵۶) نصف شد. به عبارت دیگر، محیط دایره، با اندازه شعاع و قطر آن رابطه مستقیم دارد.
مثال دوم: محاسبه محیط چرخ و فلک
چرخ و فلک «چشم لندن»، یکی از بزرگترین چرخ و فلکهای دنیا با ارتفاع ۱۳۵ متر و قطر چرخ ۱۲۰ متر است. اگر شخصی سوار این چرخ و فلک شود، پس از یک دور کامل و برگشتن به نقطه سوار شدن، چه مسافتی را طی کرده است؟ برای طی کردن مسافت ۲ کیلومتر، چرخ و فلک باید چند دور بزند؟ (عدد پی را برابر ۳ فرض کنید.)

مسافت طی شده در هر دور کامل چرخ و فلک، برابر محیط چرخ است. بنابراین، برای حل مسئله، باید فرمول محیط دایره را بنویسیم:
قطر $$times$$ عدد پی = محیط دایره
$$
C=πd
$$
- C: محیط چرخ و فلک
- π: عدد ثابت پی برابر ۳ (مطابق با فرض مسئله)
- d: قطر چرخ و فلک برابر ۱۲۰ متر
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
$$
C=3 times 120
$$
$$
C=360
$$
با هر دور کامل چرخ و فلک، افراد درون آن، مسافت معادل ۳۶۰ متر را طی میکنند. بنابراین، برای محاسبه تعداد دورهای مورد نیاز برای طی کردن مسافت ۲ کیلومتر، داریم:
۳۶۰ $$times$$ تعداد دور = مسافت طی شده
۳۶۰ $$times$$ تعداد دور = ۲۰۰۰
۳۶۰ ÷ ۲۰۰۰ = تعداد دور
۵٫۵ ≅ تعداد دور
در نتیجه، پس از حدود پنج و نیم دور، مسافت طی شده به ۲ کیلومتر (۲۰۰۰ متر) میرسد. توجه داشته باشید که پس از نیم دور، پایینترین کابین چرخ و فلک در بالاترین ارتفاع قرار میگیرد.
مثال سوم: محاسبه محیط نیم دایره
محیط نیم دایره زیر را حساب کنید. (عدد پی را برابر ۳ در نظر بگیرید.)
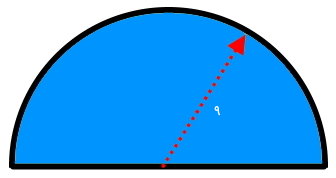
نیمدایره بالا، از یک بخش منحنی شکل و یک پارهخط راست تشکیل میشود. محیط بخش منحنی، برابر نصف محیط دایره است. اندازه پارهخط راست نیز برابر قطر است. به این ترتیب، محیط نیمدایره از رابطه زیر به دست میآید:
قطر + نصف محیط دایره = محیط نیم دایره
به منظور تعیین نصف محیط دایره، ابتدا محیط دایره کامل با شعاع ۹ را محاسبه میکنیم:
شعاع $$times$$ عدد پی $$times$$ 2 = محیط دایره
$$
C=2πr
$$
- C: محیط
- π: عدد ثابت ۳
- r: شعاع دایره برابر ۹ سانتیمتر
$$
C=2 times 3 times 9
$$
$$
C=6 times 9
$$
$$
C=54
$$
محیط دایره برابر ۵۴ است. بنابراین، نصف محیط دایره برابر ۲۷=۲÷۵۴ خواهد بود. قطر دایره نیز با دو برابر کردن شعاع دایره به دست میآید. به عبارت دیگر، قطر نیمدایره برابر ۹$$times$$2= 18 است. اکنون، اندازههای معلوم را درون رابطه محیط نیمدایره قرار میدهیم:
قطر + نصف محیط دایره = محیط نیم دایره
۱۸ + ۲۷ = محیط نیم دایره
۴۵ = محیط نیم دایره
محیط نیمدایرهای با شعاع ۹، برابر ۴۵ است.
مثال چهارم: محاسبه محیط ترکیب دو نیم دایره
تصویر زیر، ترکیبی از دو نیم دایره با شعاعهای متفاوت است. محیط این شکل را حساب کنید.
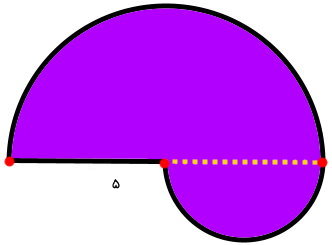
همان طور که مشاهده میکنید، شکل بالا، ترکیبی از دو نیمدایره است. با این وجود، خطچین، بخشی از محیط شکل را تشکیل نمیدهد. به این ترتیب، محیط این شکل ترکیبی عبارت است از:
شعاع دایره بزرگ + نصف محیط دایره کوچک + جمع نصف محیط دایره بزرگ = محیط شکل
انجام محاسبات را از نصف محیط دایره بزرگ شروع میکنیم:
شعاع دایره بزرگ $$times$$ عدد پی $$times$$ 2 = محیط دایره بزرگ
$$
C_b=2πr
$$
- Cb: محیط دایره بزرگ
- π: عدد ثابت ۳/۱۴
- r: شعاع دایره بزرگ برابر ۵ سانتیمتر
$$
C_b=2 times 3/14 times 5
$$
$$
C_b=6.28 times 5
$$
$$
C_b=31.4
$$
بنابراین، نصف محیط دایره بزرگ، برابر با $$۳۱٫۴ div 2 = 15.7$$ است. با توجه به شکل، شعاع دایره بزرگ با قطر دایره کوچک برابری میکند. به عبارت دیگر، شعاع دایره کوچک، نصف شعاع دایره بزرگ است. از مثال اول بخش، مشاهده کردیم که محیط دایره با شعاع آن رابطه مستقیم دارد. در نتیجه، نصف محیط دایره کوچک، برابر با نصف محیط دایره بزرگ، یعنی $$۱۵٫۷ div 2 = 7.85$$ خواهد بود. اکنون، تمام اندازههای به دست آمده را درون رابطه محیط شکل قرار میدهیم:
شعاع دایره بزرگ + نصف محیط دایره کوچک + نصف محیط دایره بزرگ = محیط شکل
۵ + ۷٫۸۵ + ۱۵٫۷ = محیط شکل
۲۸٫۵۵ = محیط شکل
محیط شکل برابر ۲۸/۵۵ است.
مثال پنجم: محاسبه محیط سه چهارم دایره
تصویر زیر، شکل سه چهارم دایره با شعاع ۱۰ را نمایش میدهد. محیط این شکل را بدست آورید. (عدد پی را برابر ۳ در نظر بگیرید.)

با توجه به تصویر بالا، محیط سه چهارم دایره، برابر است با:
شعاع + شعاع + سه چهارم محیط دایره کامل = محیط سه چهارم دایره
سه چهارم محیط دایره را با استفاده از فرمول زیر محاسبه میکنیم:
$$frac {3} {4} times 2 times 3 times 10$$ = محیط سه چهارم دایره
$$frac {3} {2}times 3 times 10$$ = محیط سه چهارم دایره
$$۳times 3 times 5$$ = محیط سه چهارم دایره
۴۵ = محیط سه چهارم دایره
عدد بالا را به همراه اندازه شعاع در رابطه محیط سه چهارم دایره قرار میدهیم:
۱۰ + ۱۰ + ۴۵ = محیط سه چهارم دایره
۶۵ = محیط سه چهارم دایره
در نتیجه، محیط سه چهارم دایره برابر ۶۵ است.
مثال ششم: محاسبه محیط ترکیب نیم دایره و مثلث متساوی الاضلاع
تصویر زیر، شکلی را نمایش میدهد که ترکیبی از نیمدایره و مثلث متساوی الاضلاع است. اگر قطر نیمدایره برابر ۱۲ باشد، محیط شکل چقدر خواهد بود؟

با توجه به تصویر، محیط شکل ترکیبی بالا برابر است با:
ضلع مثلث + ضلع مثلث + نصف محیط دایره = محیط شکل
نصف محیط دایره از رابطه زیر محاسبه میشود:
$$frac {1} {2} times 3/14 times 12$$ = نصف محیط دایره
$$۳/۱۴ times 6$$ = نصف محیط دایره
۱۸٫۸۴ = نصف محیط دایره
در مثلث متساوی الاضلاع، اندازه تمام ضلعها با هم برابر هستند. از آنجایی که یکی از ضلعهای این مثلث (خط چین)، بر روی قطر نیمدایره قرار دارد، اندازه تمام ضلعهای مثلث برابر با ۱۲ خواهد بود. اندازههای به دست آمده را درون رابطه محیط شکل قرار میدهیم:
۱۲ + ۱۲ + ۱۸٫۸۴ = محیط شکل
۴۲٫۸۴ = محیط شکل
محیط شکل ترکیبی برابر ۴۲/۸۴ است.
مثال هفتم: مقایسه محیط دایره با چند ضلعی محاط در دایره
تصویر زیر، یک مربع، یک شش ضلعی منتظم و یک هشت ضلعی منتظم محاط در دایرهای به شعاع ۱۵ سانتیمتر را نمایش میدهد. محیط کدام چند ضلعی به محیط دایره نزدیکتر است؟ از این مقایسه، چه نتیجهای میتوان گرفت؟
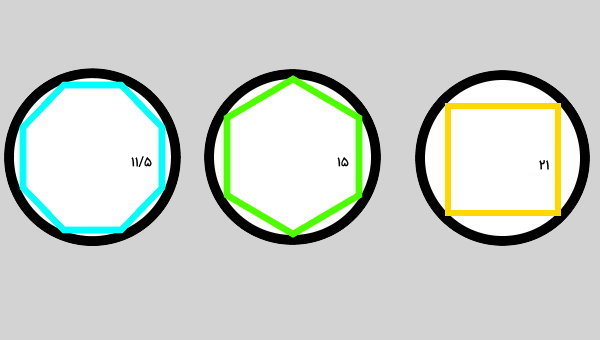
برای مقایسه محیط شکلهای محاطی، ابتدا محیط دایره را محاسبه میکنیم:
شعاع $$times$$ عدد پی $$times$$ 2 = محیط دایره
$$
C=2πr
$$
- C: محیط
- π: عدد ثابت ۳/۱۴
- r: شعاع دایره برابر ۱۵ سانتیمتر
$$
C=2 times 3/14 times 15
$$
$$
C=2 times 3/14 times 15
$$
$$
C=94.25
$$
محیط دایره محیطی برابر ۹۴٫۲۵ سانتیمتر است. از آنجایی که شکلهای محاطی از نوع چند ضلعی منتظم هستند، محیط آنها از ضرب تعداد اضلاع در اندازه هر ضلع به دست میآید:
ضلع مربع $$ times $$ 4 = محیط مربع
ضلع شش ضلعی $$ times $$ 6 = محیط شش ضلعی
ضلع هشت ضلعی $$ times $$ 4 = محیط هشت ضلعی
اندازه ضلع هر شکل را در فرمول مربوط به آن قرار میدهیم:
۸۴ = ۲۱ $$ times $$ 4 = محیط مربع
۹۰ = ۱۵ $$ times $$ 6 = محیط شش ضلعی
۹۲ = ۱۱٫۵ $$ times $$ 8 = محیط هشت ضلعی
همانطور که مشاهده میکنید، هر چه تعداد ضلعهای چند ضلعی محاط در دایره بیشتر و اندازه ضلعها کمتر باشد، محیط آن چند ضلعی به محیط دایره نزدیکتر است. به این ترتیب، میتوان نتیجه گرفت که محیط یک چند ضلعی منتظم محیط در دایره با بینهایت ضلع، برابر با محیط دایره محیطی خواهد بود.
مثال هشتم: محاسبه محیط دایره با مساحت
محیط دایرهای به مساحت ۱۲ متر مربع حساب کنید. (عدد پی را برابر ۳ در نظر بگیرید.)
فرمول محیط دایره بر حسب مساحت به صورت زیر نوشته میشود:
$$
C=2 sqrt{pi A}
$$
- C: محیط
- A: مساحت دایره برابر ۱۲ متر مربع
- π: عدد ثابت برابر ۳ (مطابق فرض مسئله)
اندازهای معلوم را در فرمول بالا قرار میهیم:
$$
C=2 sqrt{ 3 times 12}
$$
$$
C=2 sqrt{ 36 }
$$
$$
C = 2 times 6
$$
$$
C = 12
$$
در نتیجه، محیط دایرهای با مساحت ۱۲ متر مربع، حدودا برابر ۱۲ متر است (به دلیل فرض ۳ بودن عدد پی، محیط به دست آمده، تقریبی است).
محاسبه آنلاین محیط دایره
در این مقاله، روشهای مختلف محیط دایره در حالتهای مختلف را آموزش دادیم. یکی از روشهای محاسبه محیط شکلهای مختلف هندسی، استفاده از سایتهای اینترنتی عمومی و تخصصی نظیر موتور جستجوی Google (+)، سایت Omni Calculator (+) و سایت Calculator.net (+) است.
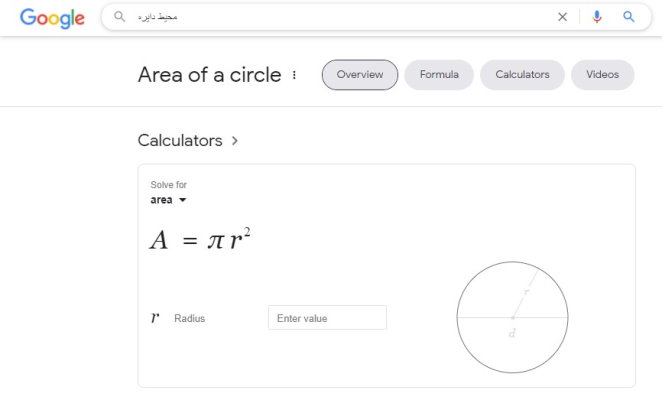
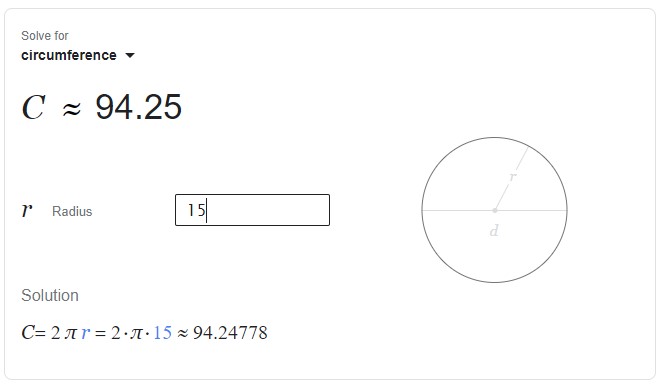
در صورت جستجوی عبارت «محیط دایره» یا «Circumference»، کادری مشابه تصویر بالا در ابتدای صفحه نتایج گوگل ظاهر میشود. این کادر، ضمن نمایش فرمول محیط دایره، امکان محاسبه مقدار آن با وارد کردن شعاع را فراهم میکند. به عنوان مثال، اگر عدد ۱۵ را به عنوان شعاع دایره مورد نظر درون کادر مقابل عنوان «r Radius» وارد کنیم، محیط دایره و روند محاسبه آن به نمایش در میآید.
سوالات متداول در رابطه با محیط دایره
در این بخش، به برخی از سوالات پرتکرار در زمینه محیط دایره، و نحوه محاسبه آن پاسخ میدهیم.
فرمول محیط دایره با شعاع چیست؟
فرمول محیط دایره با شعاع، C=2πr (دو پی آر) است. در این فرمول، r، شعاع دایره و π، عدد ثابت ۳/۱۴ را نمایش میدهد.
فرمول محیط دایره با قطر چیست؟
فرمول محیط دایره با قطر، C=πd (پی دی) است. در این فرمول، d، قطر دایره π، عدد ثابت ۳/۱۴ را نمایش میدهد.
محیط دایره چند درجه است؟
محیط دایره کامل برابر ۳۶۰ درجه است.
محیط دایره چند رادیان است؟
محیط دایره کامل برابر ۲π یا ۶/۲۸ رادیان است.
طول کمان دایره چگونه بدست می آید ؟
طول کمان دایره از ضرب زاویه مقابل کمان در شعاع دایره به دست میآید. زاویه در اینجا بر حسب رادیان بیان میشود.
محیط قطاع دایره چگونه بدست می آید ؟
محیط قطاع دایره از جمع طول کمان قطاع با قطر دایره به دست میآید.
+ در ریسمونک بخخوانید:
دانلود مجموعه سوالات معادلات دیفرانسیل






