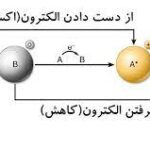
مساحت مثلث با سینوس چگونه محاسبه می شود ؟

مساحت مثلث با سینوس با استفاده از روابط مثلثاتی و قانون سینوس‌ها محاسبه می‌شود. شناخته شده‌ترین رابطه تعیین مساحت مثلث با سینوس، ضرب اندازه‌های هر دو ضلع مثلث در سینوس زاویه بین آن‌ها است. در این مقاله، فرمول‌های محاسبه مساحت مثلث با سینوس در حالت‌های مختلف (دو ضلع و زاویه بین، دو زاویه و ضلع بین، دو ضلع و زاویه غیر بین) را به همراه مثال آموزش می‌دهیم. در انتها نیز، جدولی را برای مرور این فرمول‌ها ارائه می‌کنیم.

مثلث چیست؟

مثلث (به انگلیسی Triangle)، یکی از شناخته‌شده‌ترین و پرکاربردترین شکل‌های هندسی چند ضلعی است که به عنوان مبنای علم مثلثات در نظر گرفته می‌شود. این چند ضلعی، سه ضلع و سه راس دارد.

 

 

مساحت مثلث چیست؟

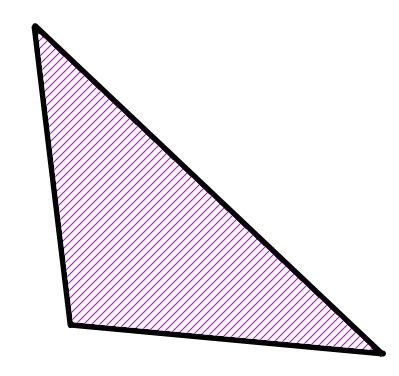
مساحت مثلث، کمیتی است که اندازه سطح داخل ضلع‌های مثلث را نمایش می‌دهد. در تصویر زیر، میزان محدوده هاشور خورده، همان مساحت مثلث است.

 

 

روش های محاسبه مساحت مثلث چه هستند؟

به طور کلی، سه روش کلی برای تعیین مساحت تمام انواع مثلث‌ها وجود دارد. این سه روش عبارت هستند از:

• محاسبه مساحت مثلث با قاعده و ارتفاع
• محاسبه مساحت مثلث با سه ضلع (روش هرون)
• محاسبه مساحت مثلث با سینوس (روش مثلثاتی)

مساحت مثلث با سینوس چگونه بدست می آید ؟

مساحت مثلث با سینوس توسط روابط مثلثاتی مخصوص به دست می‌آید. تصویر زیر، ضلع‌ها و زوایای یک مثلث را با حروه انگلیسی نمایش می‌دهد.

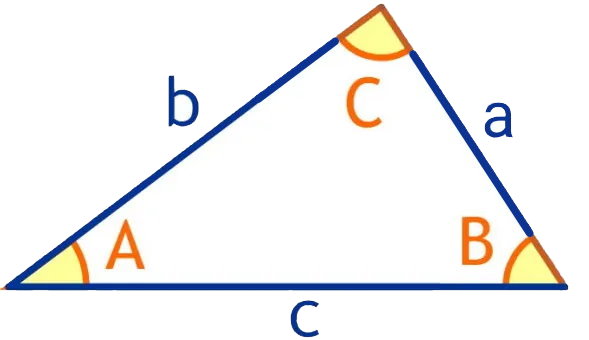
مثلث بالا از نظر مشخص بودن اندازه ضلع‌ها و زوایا، به انواع زیر تقسیم می‌شود:

• مثلث ض ز ض: مثلث با دو ضلع و زاویه بین معلوم
• مثلث ز ض ز: مثلث با دو زاویه و ضلع بین معلوم
• مثلث ض ض ز: مثلث با دو ضلع و زاویه غیر بین معلوم
• مثلث ز ز ض: مثلث با دو زاویه و ضلع غیر بین معلوم
• مثلث ض ض ض: مثلث با سه ضلع معلوم (محاسبه مساحت این مثلث به روش هرون انجام می‌شود.)
• مثلث ز ز ز: مثلث با سه زاویه معلوم (محاسبه مساحت این مثلث غیر ممکن است.)

فرمول مساحت مثلث با سینوس چیست ؟

فرمول مساحت مثلث با سینوس به حالت مثلث بستگی دارد. مساحت مثلث با دو ضلع و زاویه بین توسط یکی از فرمول‌های زیر محاسبه می‌شود:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}a\cdot b\cdot sinC$$

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}a\cdot c\cdot sinB$$

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}b\cdot c\cdot sinA$$

• Area: مساحت
• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB
• A: زاویه راس A
• B: زاویه راس B
• C: زاویه راس C

فرمول‌های محاسبه مساحت مثلث با دو زاویه و ضلع بین نیز عبارت هستند از:

$$\text{Area}=\frac{c^{\mathrm{۲}}\cdot sinA\cdot sinB}{\mathrm{۲}\cdot sin(A+B)}$$

$$\text{Area}=\frac{b^{\mathrm{۲}}\cdot sinA\cdot sinC}{\mathrm{۲}\cdot sin(A+C)}$$

$$\text{Area}=\frac{a^{\mathrm{۲}}\cdot sinB\cdot sinC}{\mathrm{۲}\cdot sin(B+C)}$$

نکته: در کسر فرمول‌های بالا، امکان استفاده از زاویه سوم به جای جمع دو زاویه وجود دارد (مانند زوایه C به جای A+B). مقدار زاویه سوم از قانون جمع زوایای داخلی، به دست می‌آید.

فرمول‌های مساحت مثلث‌های ض ز ض و ز ض ز به عنوان فرمول مساحت مثلث با سینوس شناخته می‌شود. برای نوشتن این فرمول‌ها، نیازی به تعیین پارامترهای اضافی یا نوشتن روابط دیگر نیست. با این وجود، شرایط برای مثلث‌های دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین کمی تفاوت دارد. در این مثلث‌ها، ابتدا باید ضلع‌ها و زوایای دیگر را با استفاده از قانون سینوس‌ها به دست آورد. مطابق با این قانون داریم:

$$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$$

با داشتن دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین، می‌توان اندازه‌های دیگر را به کمک نسبت‌های بالا تعیین کرد و مساحت مثلث را به دست آورد. در بخش بعدی، برای حالت‌های مختلف، چند مثال ارائه و حل می‌کنیم.

مثال های محاسبه مساحت مثلث با سینوس

در این بخش، به حل سه مثال برای حالت‌های مختلف محاسبه مساحت مثلث با سینوس (دو ضلع و زاویه بین، دو زاویه و ضلع بین و دو ضلع و زاویه غیر بین) می‌پردازیم.

مثال اول: مساحت مثلث با دو ضلع و زاویه بین

مثلثی با دو ضلع ۱۰ سانتی‌متر و ۷ سانتی‌متر را در نظر بگیرد. اگر زاویه بین این دو ضلع برابر ۳۰ درجه باشد، مساحت مثلث چقدر خواهد بود؟

به دلیل مشخص بودن اندازه دو ضلع و زاویه بین، فرمول مساحت مثلث با سینوس برای حالت ض ز ض را می‌نویسیم:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}a\cdot b\cdot sinC$$

• Area: مساحت
• a: اندازه یکی از ضلع‌ها برابر ۱۰ سانتی‌متر
• b: اندازه ضلع دیگر برابر ۷ سانتی‌متر
• C: زاویه بین دو ضلع معلوم برابر ۳۰ درجه

اندازه‌های معلوم را درون رابطه بالا قرار می‌دهیم:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}\times \mathrm{۱۰}\times \mathrm{۷}\times sin\mathrm{۳۰}°$$

سینوس زاویه ۳۰ درجه برابر یک دوم است:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}\times \mathrm{۱۰}\times \mathrm{۷}\times \frac{\mathrm{۱}}{\mathrm{۲}}$$

$$Area=\mathrm{۵}\times \mathrm{۷}\times \frac{\mathrm{۱}}{\mathrm{۲}}$$

$$Area=\mathrm{۳۵}\times \frac{\mathrm{۱}}{\mathrm{۲}}$$

$$Area=\mathrm{۱۷.۵}$$

مثال دوم: مساحت مثلث با دو زاویه و ضلع بین

مثلثی با دو زاویه ۴۵ درجه را در نظر بگیرید. اگر طول ضلع بین این دو زاویه برابر ۱۴ سانتی‌متر باشد، مساحت مثلث چقدر خواهد بود؟

به دلیل مشخص بودن دو زاویه و ضلع بین آن‌ها، از فرمول مساحت مثلث با سینوس برای حالت ز ض ز استفاده می‌کنیم:

$$\text{Area}=\frac{c^{\mathrm{۲}}\cdot sinA\cdot sinB}{\mathrm{۲}\cdot sin(A+B)}$$

• Area: مساحت
• c: اندازه ضلع بین دو زاویه معلوم برابر ۱۴
• A: اندازه یکی از زوایای معلوم برابر ۴۵ درجه
• B: اندازه دیگر زاویه معلوم برابر ۴۵ درجه

اندازه‌های بالا را درون فرمول قرار می‌‌دهیم:

$$\text{Area}=\frac{{\mathrm{۱۴}}^{\mathrm{۲}}\times sin\mathrm{۴۵}°\cdot sin\mathrm{۴۵}°}{\mathrm{۲}\times sin(\mathrm{۴۵}°+\mathrm{۴۵}°)}$$

$$\text{Area}=\frac{{\mathrm{۱۴}}^{\mathrm{۲}}\times sin\mathrm{۴۵}°\cdot sin\mathrm{۴۵}°}{\mathrm{۲}\times sin\left(\mathrm{۹۰}°\right)}$$

سینوس زاویه ۴۵ درجه برابر $$\frac{\sqrt{\mathrm{۲}}}{\mathrm{۲}}$$

و سینوس زاویه ۹۰ درجه برابر ۱ است:

$$\text{Area}=\frac{\mathrm{۱۹۶}\times \frac{\sqrt{\mathrm{۲}}}{\mathrm{۲}}\times \frac{\sqrt{\mathrm{۲}}}{\mathrm{۲}}}{\mathrm{۲}\times \mathrm{۱}}$$

$$\text{Area}=\mathrm{۹۸}\times \frac{\sqrt{\mathrm{۲}}\times \sqrt{\mathrm{۲}}}{\mathrm{۲}\times \mathrm{۲}}$$

$$\text{Area}=\mathrm{۹۸}\times \frac{\mathrm{۲}}{\mathrm{۴}}$$

$$\text{Area}=\mathrm{۹۸}\times \frac{\mathrm{۱}}{\mathrm{۲}}$$

$$\text{Area}=\mathrm{۴۹}$$

در نتیجه، مساحت مثلث برابر ۴۹ سانتی‌متر مربع است. توجه داشته باشید که به دلیل وجود دو زاویه ۴۵ درجه، زاویه سوم برابر ۹۰ درجه خواهد بود. به عبارت دیگر، مثلث مورد سوال، از نوع قائم الزاویه بود. به علاوه، برابر بودن دو زاویه، متساوی الساقین بودن مثلث (برابر بودن اندازه ساق‌ها) را نمایش می‌دهد. در صورت تمایل می‌توانید با در نظر گرفتن این نکات و استفاده از قضیه فیثاغورس، مسئله حل کنید. در هر صورت، جواب مسئله یکسان خواهد بود.

مثال سوم: مساحت مثلث با دو ضلع و زاویه غیر بین

مساحت مثلث نمایش داده شده در تصویر زیر را به دست بیاورید. از اطلاعات زیر برای حل مسئله استفاده کنید:

• sin 31°≅۰٫۵۱
• sin 57°≅۰٫۸۳
• sin 92°≅۱

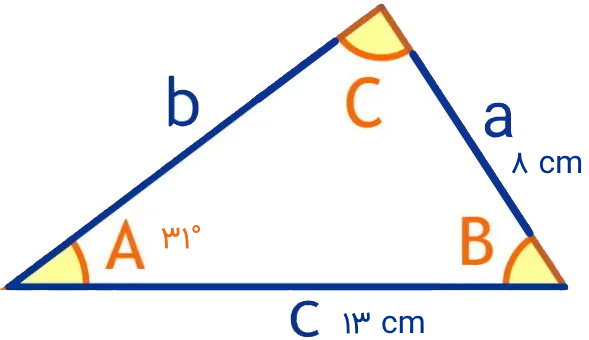
در حالت دو ضلع و زاویه بین، اولین مرحله، نوشتن قانون سینوس‌ها و تعیین پارامترهای مجهول است:

$$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$$

بر اساس تصویر بالا، داریم:

• a=8
• c=13
• A=31°

این مقادیر را در تناسب بالا قرار می‌‌دهیم:

$$\frac{\mathrm{۸}}{sin\mathrm{۳۱}°}=\frac{b}{sinB}=\frac{\mathrm{۱۳}}{sinC}$$

$$\frac{\mathrm{۸}}{sin\mathrm{۳۱}°}=\frac{\mathrm{۱۳}}{sinC}$$

$$\frac{\mathrm{۸}}{\mathrm{۰٫۵۱}}=\frac{\mathrm{۱۳}}{sinC}$$

$$\sin C=\frac{\mathrm{۱۳}\times \mathrm{۰٫۵۱}}{\mathrm{۸}}$$

$$\sin C=\mathrm{۰.۸۳}$$

با توجه به اطلاعات مسئله و مقدار به دست آمده از محاسبات بالا، زاویه C برابر ۵۷ درجه خواهد بود. این زاویه نیز مانند زاویه A، در بین ضلع‌های a و c قرار ندارد. با این وجود، بر اساس قانون جمع زوایای داخلی، این زاویه به محاسبه زاویه B کمک می‌کند:

$$A+B+C=\mathrm{۱۸۰}°$$

$$\mathrm{۵۷}°+B+\mathrm{۳۱}°=\mathrm{۱۸۰}°$$

$$B+\mathrm{۸۸}°=\mathrm{۱۸۰}°$$

$$B=\mathrm{۱۸۰}°–\mathrm{۸۸}°$$

$$B=\mathrm{۹۲}°$$

زاویه B برابر ۹۲ درجه است. اکنون تمام زوایای مثلث معلوم هستند. در صورت تمایل می‌توان ضلع b را نیز با استفاده از قانون سینوس‌ها محاسبه کرد. البته برای محاسبه مساحت مثلث، داشتن ضلع‌های a و c با زاویه بین آن‌ها (B) کفایت می‌کند. به همین دلیل، فرمول مساحت مثلث برای این حالت (ض ز ض) را می‌نویسیم:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}a\cdot c\cdot sinB$$

اندازه‌های موجود و به دست آمده را درون فرمول بالا قرار می‌دهیم:

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}\times \mathrm{۸}\times \mathrm{۱۳}\times sin\mathrm{۹۲}°$$

$$Area=\frac{\mathrm{۱}}{\mathrm{۲}}\times \mathrm{۸}\times \mathrm{۱۳}\times \mathrm{۱}$$

$$Area=\mathrm{۴}\times \mathrm{۱۳}$$

$$Area=\mathrm{۵۲}$$

مساحت مثلث برابر ۵۲ سانتی‌متر مربع است.

جدول فرمول های مساحت مثلث با سینوس

فرم‌های مختلف نوشتن فرمول مساحت مثلث با سینوس بر اساس انداز‌های مشخص در جدول زیر آورده شده‌اند.