توان در متمتیکا – با مثال های فراوان

نرم افزار متمتیکا چیست؟

متمتیکا یک سیستم نرم‌افزاری با کتابخانه‌های داخلی برای چندین حوزه محاسبات فنی است که امکان یادگیری ماشین، آمار، محاسبات نمادین، دستکاری ماتریس‌ها، ترسیم توابع و انواع مختلف داده، پیاده‌سازی الگوریتم‌ها، ایجاد رابط‌های کاربری و رابط کاربری برای برنامه نویسی در زبان‌های دیگر را فراهم می‌کند. ایده این نرم افزار توسط «استفان ولفرام» (Stephen Wolfram) مطرح شد و توسط کمپانی ولفرام توسعه داده شد. زبان ولفرام زبان مورد استفاده در متمتیکا است.

برای آشنایی بیشتر با نرم افزار متمتیکا می‌توانید، مطلب متمتیکا چیست که پیش از این در مجله فرادرس منتشر شده است را مطالعه کنید.

رابط دفترچه یادداشت

ولفرام متمتیکا که توسط برخی از کاربران آن متمتیکا نامیده می‌شود، به دو بخش تقسیم می‌شود: کرنل و فرانت اند. کرنل یا هسته عبارات (کد زبان ولفرام) را تفسیر می‌کند و نتیجه را برمی‌گرداند، که سپس می‌تواند توسط قسمت فرانت اند نمایش داده شود.

فرانت اند اصلی، که توسط تئودور گری در سال ۱۹۸۸ طراحی شد، شامل یک رابط نوت بوک است و امکان ایجاد و ویرایش اسناد نوت بوک را فراهم می‌کند که می‌تواند شامل کد، متن ساده، تصاویر و گرافیک باشد.

جایگزین اصلی فرانت اند متمتیکا عبارت از «ولفرام ورکبنچ» (Wolfram Workbench) است که یک محیط توسعه یکپارچه مبتنی بر اکلیپس است و در سال ۲۰۰۶ معرفی شد. این ابزار روش‌هایی برای توسعه کد مبتنی بر پروژه را برای متمتیکا، از جمله مدیریت بازنگری، اشکال زدایی، پروفایل و آزمایش فراهم می‌کند.

همچنین یک پلاگین برای IDEهای مبتنی بر IntelliJ IDEA برای کار با کد زبان ولفرام وجود دارد که علاوه بر برجسته کردن نحو می‌تواند متغیرهای محلی و توابع تعریف شده را تجزیه و تحلیل و به صورت خودکار تکمیل کند. هسته یا کرنل متمتیکا همچنین شامل خط فرمان در فرانت اند است.

رابط های دیگر متمتیکا عبارت از JMath بر اساس خط خوانش GNU و ولفرام اسکریپت است که برنامه‌های خودکار متمتیکا را از خط فرمان UNIX اجرا می‌کند.

محاسبات با کارایی بالا

قابلیت‌های محاسبات با کارایی بالا با معرفی آرایه‌های طبقه بندی شده در نسخه ۴ (۱۹۹۹) و ماتریس‌های پراکنده یا sparse در نسخه ۵ (۲۰۰۳) و با استفاده از کتابخانه‌های مختلف و انجام محاسبات با دقت بالا، فراهم آمد.

در نسخه $$\mathrm{۵٫۲}$$

(۲۰۰۵) هنگامی که محاسبات بر روی رایانه‌های چند هسته‌ای انجام شد، چند رشته خودکار را اضافه کرد. این نسخه شامل کتابخانه‌های بهینه سازی شده مخصوص CPU بود. علاوه بر این متمتیکا توسط سخت افزار شتاب دهنده سوم شخص مانند ClearSpeed ​​نیز پشتیبانی می‌شود.

در سال ۲۰۰۲، گرید متمتیکا معرفی شد تا برنامه‌نویسی موازی در سطح کاربر را بر روی خوشه‌های ناهمگن و سیستم‌های چند پردازنده‌ای فراهم کند. همچنین در سال ۲۰۰۸ فناوری محاسبات موازی در تمام نسخه‌های متمتیکا شامل پشتیبانی از فناوری شبکه مانند Windows HPC Server 2008، Microsoft Compute Cluster Server و سان گرید فراهم آمد. پشتیبانی از سخت افزار GPU CUDA و OpenCL نیز در سال ۲۰۱۰ به متمتیکا اضافه شد. در سال ۲۰۱۹ نیز پشتیبانی برای کامپایل کردن کد زبان ولفرام نیز به LLVM اضافه شد.

اتصال به سایر برنامه‌ها و زبان‌های برنامه نویسی

ارتباط با سایر برنامه‌ها از طریق پروتکلی به نام پروتکل انتقال نمادین ولفرام (WSTP) انجام می‌شود. این پروتکل اجازه می‌دهد تا ارتباط بین کرنل ولفرام متمتیکا و فرانت اند صورت بگیرد و یک رابط عمومی بین کرنل و برنامه‌های کاربردی دیگر را فراهم می‌کند.

ولفرام ریسرچ آزادانه یک کیت توسعه دهنده برای پیوند برنامه‌های نوشته شده در زبان برنامه نویسی C به هسته متمتیکا از طریق WSTP با استفاده از J/Link توسعه داده است، J/Link یک برنامه جاوا است که می‌تواند از متمتیکا بخواهد محاسبات را انجام دهد. .NET/Link نیز عملکرد مشابهی دارد اما در این حالت این پیوند به جای زبان جاوا از برنامه‌های .NET صورت می‌گیرد.

زبان‌های دیگری که به متمتیکا متصل می‌شوند عبارت از هسکل، اپل اسکریپت، راکت، پایتون، ویژوآل بیسیک و Clojure هستند. متمتیکا از تولید و اجرای مدل‌های مدلیکا برای مدل‌سازی سیستم‌ها پشتیبانی می‌کند و از طریق Wolfram System Modeler متصل می‌شود. همچنین پیوندها با متمتیکا برای بسیاری از بسته‌های نرم‌افزاری رابط سوم و APIها در دسترس هستند.

متمتیکا همچنین می‌تواند داده‌های زمان واقعی را از منابع مختلف بگیرد و می‌تواند بلاک چین‌های عمومی (بیت کوین، اتریوم و ARK) را بخواند و بنویسد.

این برنامه می‌تواند از ورودی و خروجی بیش از ۲۲۰ داده، تصویر، ویدئو، صدا، طراحی‌های CAD، سیستم‌های اطلاعات جغرافیایی (GIS)، داکیومنت و فرمت‌های زیست پزشکی پشتیبانی کند.

داده‌های قابل محاسبه

متمتیکا با ولفرام آلفا یکپارچه شده است. ولفرام آلفا یک موتور پاسخ دهی دانش محاسباتی آنلاین است که داده‌هایی را برای کاربرانی که از متمتیکا با اتصال به اینترنت استفاده می‌کنند، به‌ روز نگه می‌دارد. برخی از مجموعه داده‌ها شامل داده‌های نجومی، شیمیایی، ژئوپلیتیک، زبان، زیست پزشکی و آب و هوا، علاوه بر داده‌های ریاضی مانند گره‌ها و چند وجهی‌ها هستند.

دستاوردهای متمتیکا

بایت (BYTE) در سال ۱۹۸۹ متمتیکا را به عنوان یکی از برندگان متمایز جوایز بایت فهرست کرد و بیان کرد متمتیکا یکی دیگر از برنامه‌های پیشرفته و کاربردی مکینتاش می‌تواند شما را قادر سازد به گونه‌ای جبر، حساب دیفرانسیل و انتگرال را به آسانی درک کنید که فهم آن از یک کتاب درسی غیرممکن به نظر می‌رسد. با این حال متمتیکا به دلیل نداشتن سورس باز مورد انتقاد قرار گرفته است. ولفرام ریسرچ ادعا می‌کند که بسته بودن منبع متمتیکا برای مدل کسب‌ و کار آن و تداوم نرم‌افزار امری اساسی است.

آیا متمتیکا در زبان C  نوشته شده است؟

متمتیکا یکی از پیچیده‌ترین سیستم‌های نرم‌افزاری است که تاکنون ساخته شده است. کد منبع آن با ترکیب C و متمتیکا نوشته شده است. برای مثال برای نسخه ۵ این نرم افزار، کد کرنل شامل حدود ۱٫۵ میلیون خط زبان C و ۱۵۰,۰۰۰ خط متمتیکا است.

اساس کار متمتیکا چیست؟

متمتیکا یک نرم افزار محاسباتی است که در بسیاری از زمینه‌های علمی، مهندسی، ریاضی و محاسباتی بر اساس ریاضیات نمادین یا symbolic mathematics مورد استفاده قرار می‌گیرد.

نصب نرم افزار متمتیکا چگونه است؟

متمتیکا یک نرم افزار اپن سورس نیست و برای دسترسی به آن باید ثبت نام صورت گیرد. با این حال می‌توانید نرم افزار متمتیکا را از اینجا (+) دریافت کنید و مراحل نصب را طبق دستور العمل گفته شده انجام دهید.

MathID در نصب نرم افزار متمتیکا چیست؟

MathID یک کد شناسایی منحصر به فرد برای رایانه شما است که برای اتصال اطلاعات مجوز شما به دستگاه خاص شما استفاده می‌شود. برای ایجاد MathID مرتبط با دستگاه خود، باید در ابتدا متمتیکا را نصب کنید. برای پیدا کردن MathID در حین نصب متمتیکا گزینه Other ways to activate را انتخاب کنید و سپس گزینه Activate manually را برگزینید.

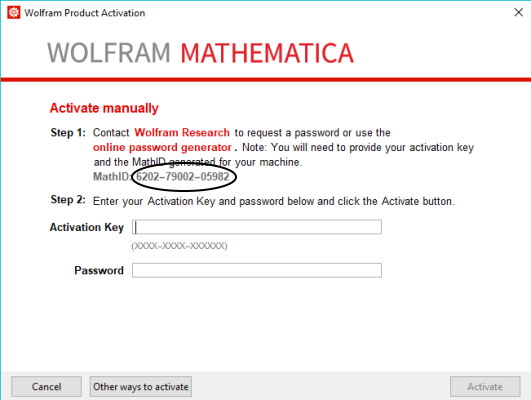
در تصویر بالا MathID نشان داده شده است. بعد از نصب متمتیکا نیز در قسمت نوت بوک متمتیکا با تایپ دستور $MachineID و اجرای آن می‌توانید به MathID سیستم خود دسترسی پیدا کنید.

شروع با نرم افزار متمتیکا

با باز کردن پنجره متمتیکا می‌توان دید که با تایپ کردن هر عدد روبروی آن یک کروشه باز می‌شود و به هر یک از این کروشه‌ها یک cell می‌گوییم. در ابتدا و برای شروع به کار در متمتیکا استفاده از دستور زیر:

Clear["Global`*"]

حافظه متمتیکا را پاک می‌کند تا اگر متغیری در آن وجود دارد در محاسبات بعدی اختلال ایجاد نکند. همچنین با دستور clear با اسم یک متغیر مشخص می‌توانیم فقط آن متغیر را از حافظه متمتیکا پاک کنیم. برای ایجاد cell‌های مختلف در صفحه می‌توان دید که نشانگر در هر cell به صورت عمودی است.

زمانی که از سل بیرون بیایید، نشانگر به صورت افقی خواهد بود و با کلیک کردن در این حالت یک cell جدید ایجاد می‌شود. برای غیرفعال کردن یک دستور در متمتیکا نیز از قسمت ادیت بالای صفحه نرم افزار گزینه Un/Comment Selection را انتخاب می‌کنیم.

دو دستور دیگر که در متمتیکا می‌تواند کمک کننده باشد، دو دستور به صورت زیر هستند:

Names ["Global`*"]
Remove ["Global`*"]

این دو دستور به ترتیب تمام کمیت‌های نامگذاری شده در متمتیکا و حذف تمام متغیرها در متمتیکا را به همراه دارد. روی هر یک از دستورات نرم افزار و با انتخاب آن‌ها می‌توان کلید F1 را استفاده کرد و بدین ترتیب وارد قسمت help نرم افزار می‌شویم که اطلاعات لازم برای هر دستور در این قسمت داده شده است. همچنین دقت داشته باشید که حرف همه دستورات باید بزرگ باشد.

اجرای دستورات در متمتیکا

برای اجرای هر cell نیز از دکمه‌های shift+enter استفاده می‌کنیم. همچنین برای اینکه مقدار متغیری که تعریف کرده‌ایم بعد از اجرای cell نمایش داده نشود لازم است در انتهای تعریف متغیر از ؛ استفاده کنیم و در این صورت بعد از اجرای کد، آن قسمت در خروجی چاپ نمی‌شود.

اگر در حین اجرای برنامه و قبل از اتمام آن بخواهید اجرای برنامه را متوقف کنید باید از گزینه Evaluation و انتخاب Quit kernel استفاده کنید. بدین ترتیب می‌توانید اجرای برنامه را در وسط محاسبات آن متوقف کنید.

دستورات در متمتیکا باید با حروف اول بزرگ نوشته شوند. همچنین دستورات باید در داخل براکت باشند.

تغییر متغیر در متمتیکا

تغییر متغیر به راحتی در متمتیکا صورت می‌گیرد. فرض کنید که عبارت f را به صورت زیر در متمتیکا تعریف کرده‌اید:

In[5]:= Clear["Global`*"]
Remove["Global`*"]
f = x^2 + x + 1

Out[7]= 1 + x + x^2

برای تغییر متغیر $$x$$

به برای مثال $$y+\mathrm{۱}$$

کافی است به صورت زیر عمل کنیم و داریم:

In[12]:= Clear["Global`*"]
Remove["Global`*"]
f = x^2 + x + 1
x = y + 1
f


Out[14]= 1 + x + x^2

Out[15]= 1 + y

Out[16]= 2 + y + (1 + y)^2

و بدین ترتیب تغییر متغیر در f صورت می‌گیرد. روش دیگر برای تغییر متغیر استفاده از دستور خط-نقطه است که به صورت زیر عمل می‌کند و در این صورت برای تغییر متغیر داریم:

In[17]:= Clear["Global`*"]
Remove["Global`*"]
g = z^2 + z + 1
g /. z -> (v + 1)



Out[19]= 1 + z + z^2

Out[20]= 2 + v + (1 + v)^2

تفاوت این دو روش در این است که در حالت اول هر جا شما عبارت f را بنویسید، نتیجه به صورت تابعی از y یعنی با تغییر متغیر، نمایش داده می‌شود. اما در حالت دوم این تغییر متغیر فقط یکبار و بعد از اجرای دستور خط-نقطه رخ می‌دهد و در حالت‌های دیگر تابع به شکل اصلی خود خواهد بود.

برای نمایش خروجی در متمتیکا نیز از دو روش می‌توان خروجی را نمایش داد که این دو روش را در ادامه نشان خواهیم داد:

In[21]:= Clear["Global`*"]
Remove["Global`*"]
a = 1/3
b = N[1/3, 5]


Out[23]= 1/3

Out[24]= 0.33333

در حالت اول و برای a می‌توان دید که نتیجه به صورت کسری نمایش داده شده است، در حالت دوم و برای b و با دستور N جواب به صورت اعشاری و با تعداد اعشارهایی که مشخص کرده‌ایم نمایش داده خواهد شد.

جذر در متمتیکا

برای محاسبه جذر در متمتیکا به دو روش می‌توان عمل کرد، اولین روش این است که از دستور Sqrt استفاده کنیم و مقداری که می‌خواهیم جذر گرفته شود در یک براکت قرار دهیم. همچنین با استفاده از کلید ctrl+2 نیز علامت رادیکال را در متمتیکا خواهیم داشت و در زیر رادیکال می‌توانیم مقداری که قرار است جذر گرفته شود را تایپ کنیم. این دو حالت در زیر نمایش داده شده است:

In[9]:= Clear["Global`*"]
Remove["Global`*"]
Sqrt[4]
Sqrt[4]


Out[11]= 2

Out[12]= 2

اگر جذری که می‌خواهیم انجام شود به صورت متغیری باشد و بخواهیم جواب جذر نمایش داده شود نیز به صورت زیر عمل می کنیم:

In[13]:= Clear["Global`*"]
Remove["Global`*"]
Sqrt[x^2]
Simplify[%, x < 0]



Out[15]= Sqrt[x^2]

Out[16]= -x

همان طور که می‌بینید قبل از دستور Simplify جواب جذری بدون محاسبه چاپ شده است اما با دستور Simplify و استفاده از علامت % که به خط آخر برنامه اشاره می‌کند و با شرط $$x>\mathrm{۰}$$

جواب رادیکال محاسبه و چاپ می‌شود. همچنین برای تعریف تابع نمایی در متمتیکا نیز از تابع Exp استفاده می‌کنیم و داریم:

In[17]:= Clear["Global`*"]
Remove["Global`*"]
Exp[2]
Exp[2] // N

Out[19]= E^2

Out[20]= 7.38906

در دستورات بالا می‌توانید تفاوت در دستورها و تفاوت در خروجی‌ها را مشاهده کنید. برای به دست آوردن جزء صحیح یک ورودی در متمتیکا از دستور Floor استفاده می‌کنیم. بدین ترتیب برای استفاده از این دستور به صورت زیر عمل خواهیم کرد:

In[21]:= Clear["Global`*"]
Remove["Global`*"]
Floor[2.3]


Out[25]= 2

برای محاسبه قدر مطلق یک مقدار نیز از دستور Abs استفاده می‌کنیم. تابع تعیین علامت نیز در متمتیکا Sign است. این تابع به ازای مقادیر منفی عدد $$-\mathrm{۱}$$

، به ازای صفر عدد $$\mathrm{۰}$$ و به ازای اعداد مثبت عدد $$+\mathrm{۱}$$

را نمایش می‌دهد. بدین ترتیب داریم:

In[26]:= Clear["Global`*"]
Remove["Global`*"]
Sign[{-2, 0, 3}]

During evaluation of In[26]:= Remove::rmnsm: There are no symbols matching "Global`*".

Out[28]= {-1, 0, 1}

برای تعریف فاکتوریل در متمتیکا نیز به دو روش می‌توان عمل کرد از طریق Factorial [x] یا از طریق $$x!$$

. هر یک از این دو روش مقدار فاکتوریل $$x$$

را محاسبه خواهند داد.

در متمتیکا $$Log$$

را می‌توان به صورت $$Log\left[x\right]$$ نمایش داد. همچنین اگر بخواهیم لگاریتم بر پایه یک عدد مشخص محاسبه شود باید دستور را به صورت $$Log[a,x]$$

بنویسیم. در این حالت لگاریتم a بر پایه x محاسبه می‌شود.

همچنین دقت کنید که عدد نپر را با حرف بزرگ یعنی به صورت $$E$$

نمایش داده می‌شود. توابع مثلثاتی نیز در متمتیکا به صورت $$Sin\left[x\right]$$ نوشته می‌شود. عکس توابع نیز به صورت $$ArcSin\left[x\right]$$

نوشته می‌شود.

به علاوه توابع هایپربولیک نیز با $$Sinh\left[x\right]$$

نشان داده خواهد شد. زوایا در متمتیکا بر حسب رادیان هستند. برای اینکه زوایای توابع مثلثاتی را بر حسب درجه داشته باشیم باید دستور را به صورت زیر وارد کنیم:

In[12]:= Clear["Global`*"]
Remove["Global`*"]
Sin[Pi/3] // N
Sin[60] // N
Sin[60 Degree] // N


During evaluation of In[12]:= Remove::rmnsm: There are no symbols matching "Global`*".

Out[14]= 0.866025

Out[15]= -0.304811

Out[16]= 0.866025

می‌توان دید که در حالت اول سینوس ۶۰ درجه بر حسب رادیان نوشته شده، در حالت دوم سینوس ۶۰ رادیان و در حالت سوم مجدداً سینوس ۶۰ درجه محاسبه شده است.

برای انتخاب اعداد تصادفی در متمتیکا در یک بازه مشخص دستور را به صورت زیر وارد می‌کنیم:

In[17]:= RandomReal[{-1, 1}, 5]

Out[17]= {-0.44184, -0.897587, -0.969946, -0.406899, -0.754038}

همچنین اگر بخواهیم اعداد تصادفی عدد صحیح باشند کافی است دستور را به صورت زیر وارد کنیم:

In[18]:= RandomInteger[{1, 10}, 3]

Out[18]= {3, 10, 1}

برای به دست آوردن کوچکترین مضرب مشترک دو عدد از دستور LCM استفاده می‌کنیم و دو عددی که می‌خواهیم تا کوچکترین مضرب مشترک آن‌ها به دست آید را در آکولاد می‌نویسیم، یعنی برای مثال داریم:

In[23]:= LCM[15, 6]

Out[23]= 30

که نشان می‌دهد کوچکترین مضرب مشترک این دو عدد ۳۰ است. به علاوه بزرگترین مقسوم علیه مشترک دو عدد را نیز می‌توانیم با دستور GCD به دست آوریم. با دو دستور Mod و Quotient باقی مانده و مقسوم علیه دو عدد را خواهیم داشت. بدین منظور داریم:

In[24]:= Mod[15, 2]
Quotient[15, 3]

Out[24]= 1

Out[25]= 5

دستور ترکیب در متمتیکا با Binomial نوشته می‌شود و داریم:

In[26]:= Binomial[15, 3]


Out[26]= 455

در این دستور انتخاب ۳ حالت از ۱۵ حالت محاسبه می‌شود و در حقیقت به زبان ریاضی داریم:

$$\frac{\mathrm{۱۵}!}{\mathrm{۳}!\times \mathrm{۱۲}!}$$

برای به دست آوردن قسمت حقیقی یک تابع می‌توان از دستور Re استفاده کرد. اما در این حالت برای یک عبارت مشخص قسمت‌های حقیقی هر متغیری که حتی به صورت حقیقی تعریف کرده‌ایم نیز نمایش داده می‌شود. به همین دلیل از دستور Refine استفاده می‌کنیم. تفاوت این دو دستور را در ادامه مشاهده خواهید کرد:

In[27]:= z = x + Iy
Re[z]
Refine[Re[z], Element[{x, y}, Reals]]

Out[27]= Iy + x

Out[28]= Re[Iy + x]

Out[29]= x + Re[Iy]

تعریف تابع در متمتیکا

برای تعریف یک تابع دلخواه در متمتیکا از دستوری به صورت $$F[x_{]}$$

استفاده می‌کنیم و برای مقدار دهی نیز تنها دستور را به صورت $$F\left[number\right]$$ استفاده می‌کنیم. برای معرفی یک تابع با چند متغیر نیز در براکت به جای $$x$$

متغیرهای دیگر را نیز می‌نویسیم. این توابع و دستورها به صورت زیر نوشته می‌شوند و داریم:

In[33]:= Clear["Global`*"]
Remove["Global`*"]
F[x_] = x^2 + 1
F[3]
Map[F, {2, 3}]
F /@ {2, 3}
G[x_, y_] = x + y + 3
G[2, 1]

Out[35]= 1 + x^2

Out[36]= 10

Out[37]= {5, 10}

Out[38]= {5, 10}

Out[39]= 3 + x + y

Out[40]= 6

دستور Map نیز برای مقداردهی به تابع و برای بیش از یک مقدار استفاده می‌شوند.

توان در متمتیکا

برای اینکه توان یا دیگر حالت‌های نوشتاری را در متمتیکا نشان دهیم از دو طریق می توانیم عمل کنیم. در روش اول در صفحه متمتیکا مسیر زیر را دنبال کنید:

Paletts < Basic Math Assistant

در پنجره‌ای که به این طریق باز شده است می‌توانید به توان یا دیگر نوشتارهای ریاضی دسترسی پیدا کنید. بدین ترتیب به راحتی می‌توانید توان را در متمتیکا تعریف کنید.

دیگر اعمال جبری مثل جذر، انتگرال یا دیگر حروف یونانی نیز از این قسمت قابل دسترسی است. ولی غیر از این روش هر یک از این اعمال جبری یک کلید میانبر نیز دارند که شما می‌توانید از این کلید میانبر استفاده کنید.

• کلید میانبر برای توان در متمتیکا استفاده از کلیدهای ctrl+6 است.
• کلید میانبر برای زیرنویس حروف استفاده از کلیدهای ctrl+- است.
• برای تایپ کردن حروفی مانند $$\alpha$$

یا $$\beta$$

• کافی است به ترتیب کلیدهای Esc+a یا Esc+b را فشار دهید و سپس با فشردن Enter حرف مورد نظر چاپ خواهد شد.
• برای آشنایی با کلیدهای میانبر دیگر در متمتیکا کافی است نشانگر خود را بر روی عملی که می‌خواهید کلید میانبر آن را بدانید نگه دارید و کلید میانبر این دستور در این حالت نمایش داده می‌شود.

دستور دیگر برای محاسبه توان در متمتیکا استفاده از دستور Power است. بدین ترتیب برای محاسبه توان در متمتیکا به صورت زیر عمل می‌کنیم و داریم:

In[41]:= Power[2, 100]

Out[41]= 1267650600228229401496703205376

یک دستور دیگر برای نمایش توان در متمتیکا استفاده از دستور $$Superscript$$

است. در این حالت می توانیم دستور را به صورت $$Superscript[\mathrm{۲},\mathrm{۳}]$$ بنویسیم که بدین معنا است که می خواهیم $${\mathrm{۲}}^{\mathrm{۳}}$$ برسد. روش دیگر نشان دادن توان در متمتیکا استفاده از دستور $$Superscript@@\mathrm{۲},\mathrm{۳}$$ است. در این حالت مجدداً نمایش $${\mathrm{۲}}^{\mathrm{۳}}$$

را خواهیم داشت. نکته مهم این است که این دو دستور تنها نمایش اعداد توان دار را خواهند داشت و محاسبه‌ای روی آن‌‌ها انجام نمی‌شود.

رسم نمودار توان در متمتیکا

برای رسم نمودار توان در متمتیکا تنها کافی است که متغیر توان دار را تعریف کنیم و برای متغیر یک بازه تعریف کنیم. در این صورت داریم:

In[42]:= Plot[Power[x, 3], {x, 0, 5}]

در این حالت تابع $$x^{\mathrm{۳}}$$

را در بازه ۰ تا ۵ رسم می‌کنیم.

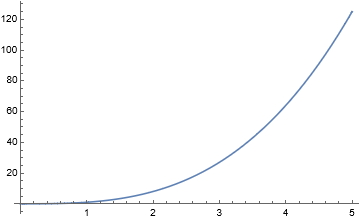
نمودار توان در متمتیکا می‌تواند سه بعدی نیز باشد. بدین منظور دستور را به صورت زیر داریم:

Clear["Global`*"]
Remove["Global`*"]
ComplexPlot3D[z^3, {z, -3 - 3 I, 3 + 3 I}, PlotLegends -> Automatic]

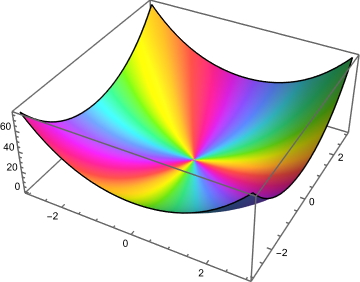
موارد احتمالی توان در متمتیکا

برای محاسبه مقدار اعداد توان دار از دستور N استفاده می‌کنیم و از % برای اشاره به خط قبلی استفاده می‌شود. برای این حالت مثال زیر را ببینید:

In[47]:= (-1)^(1/3)
N[%]

Out[47]= (-1)^(1/3)

Out[48]= 0.5 + 0.866025 I

برای مقدار دهی به توان در متمتیکا می‌توان از دستور خط-نقطه استفاده کرد. به علاوه برای ساده کردن توان در عدد از دستور PowerExpand استفاده می‌کنیم. این دو مورد را در مثال زیر نشان داده‌ایم:

In[49]:= (z^3)^(1/3)
(z^3)^(1/3) /. z -> -1
PowerExpand[(z^3)^(1/3)] 

Out[49]= (z^3)^(1/3)

Out[50]= (-1)^(1/3)

Out[51]= z

هر یک از آرایه‌های یک ماتریس‌ را می‌توان به صورت زیر به توان رساند و بدین ترتیب داریم:

In[52]:= {{1, 2}, {3, 4}}^2


Out[52]= {{1, 4}, {9, 16}}

برای به توان رساندن یک ماتریس از دستور MatrixPower استفاده می‌کنیم و داریم:

In[53]:= MatrixPower[{{1, 2}, {3, 4}}, 2]

Out[53]= {{7, 10}, {15, 22}}